代码随想录算法总结(C++)版本——单调栈
代码随想录算法总结(C++)版本——单调栈
Created: September 2, 2022 1:06 PM
739. 每日温度
请根据每日 气温 列表,重新生成一个列表。对应位置的输出为:要想观测到更高的气温,至少需要等待的天数。如果气温在这之后都不会升高,请在该位置用 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示:气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度,都是在 [30, 100] 范围内的整数。
- 情况一:当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
- 情况二:当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
- 情况三:当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
C++代码如下:
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& temperatures) {
stack<int> st;
vector<int> result(temperatures.size(),0);
st.push(0);//第一个元素的入栈
/*
情况一:当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
情况二:当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
情况三:当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
*/
//st是一个递增栈
//从栈头到栈底的顺序,栈顶元素小于等于下面的元素
for(int i=1;i<temperatures.size();i++){
if(temperatures[i]<temperatures[st.top()]){//当前元素小于栈顶元素,
st.push(i);//所以,小的入栈
}else if(temperatures[i]==temperatures[st.top()]){
st.push(i);//所以,相等也入栈的入栈
}else{//如果大于,那说明,那么上一个元素只需要隔一天就可以找到比他高的 ,i保持不变,看前面还有几个比它小的
//从而确定多少天后,会有更高的温度
while(!st.empty()&&temperatures[i]>temperatures[st.top()]){
result[st.top()]=i-st.top();
st.pop();
}
//直到i比前面的数大于等于
st.push(i);
}
}
return result;
}
};
496.下一个更大元素 I
给你两个 没有重复元素 的数组 nums1 和 nums2 ,其中nums1 是 nums2 的子集。
请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。
nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在,对应位置输出 -1 。
示例 1:
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].输出: [-1,3,-1]
接下来就要分析如下三种情况,一定要分析清楚。
- 情况一:当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
此时满足递增栈(栈头到栈底的顺序),所以直接入栈。
- 情况二:当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
如果相等的话,依然直接入栈,因为我们要求的是右边第一个比自己大的元素,而不是大于等于!
- 情况三:当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
此时如果入栈就不满足递增栈了,这也是找到右边第一个比自己大的元素的时候。
判断栈顶元素是否在nums1里出现过,(注意栈里的元素是nums2的元素),如果出现过,开始记录结果。
class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
stack<int> st;
vector<int> result(nums1.size(),-1);
unordered_map<int,int> umap;//key:元素值,value:下标
for(int i=0;i<nums1.size();i++){
umap[nums1[i]]=i;
/*
2:0
4:1
*/
}
st.push(0);//建立一个递增栈,最小的放最下面,先把第一个放进去
for(int i=1;i<nums2.size();i++){
if(nums2[i]<=nums2[st.top()]){//小于等于,都入栈
st.push(i);
}else{
while(!st.empty()&&nums2[i]>nums2[st.top()]){
//找到了比上一个元素大的元素
if(umap.count(nums2[st.top()])>0){//map是否有st.top()这个元素
int index=umap[nums2[st.top()]];//找到这个值在nums1的下标
result[index]=nums2[i];
}
st.pop();
}
st.push(i);
}
}
return result;
}
};
503.下一个更大元素II
给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
示例 1:
- 输入: [1,2,1]
- 输出: [2,-1,2]
- 解释: 第一个 1 的下一个更大的数是 2;数字 2 找不到下一个更大的数;第二个 1 的下一个最大的数需要循环搜索,结果也是 2。
// 版本一
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
// 拼接一个新的nums
vector<int> nums1(nums.begin(), nums.end());
nums.insert(nums.end(), nums1.begin(), nums1.end());
// 用新的nums大小来初始化result
vector<int> result(nums.size(), -1);
if (nums.size() == 0) return result;
// 开始单调栈
stack<int> st;
for (int i = 0; i < nums.size(); i++) {
while (!st.empty() && nums[i] > nums[st.top()]) {//nums[i]比栈顶元素大,
result[st.top()] = nums[i];//那么比栈顶大的就是nums[i]
st.pop();
}
st.push(i);
}
// 最后再把结果集即result数组resize到原数组大小
result.resize(nums.size() / 2);
return result;
}
};
走两遍
// 版本二
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
vector<int> result(nums.size(), -1);
if (nums.size() == 0) return result;
stack<int> st;
for (int i = 0; i < nums.size() * 2; i++) {
// 模拟遍历两边nums,注意一下都是用i % nums.size()来操作
while (!st.empty() && nums[i % nums.size()] > nums[st.top()]) {
result[st.top()] = nums[i % nums.size()];
st.pop();
}
st.push(i % nums.size());
}
return result;
}
};
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

- 输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
- 输出:6
- 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
双指针:
class Solution {
public:
int trap(vector<int>& height) {
int sum = 0;
for (int i = 0; i < height.size(); i++) {
// 第一个柱子和最后一个柱子不接雨水
if (i == 0 || i == height.size() - 1) continue;
int rHeight = height[i]; // 记录右边柱子的最高高度
int lHeight = height[i]; // 记录左边柱子的最高高度
for (int r = i + 1; r < height.size(); r++) {
if (height[r] > rHeight) rHeight = height[r];
}
for (int l = i - 1; l >= 0; l--) {
if (height[l] > lHeight) lHeight = height[l];
}
int h = min(lHeight, rHeight) - height[i];
if (h > 0) sum += h;
}
return sum;
}
};
动态规划解法:
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0;
vector<int> maxLeft(height.size(), 0);
vector<int> maxRight(height.size(), 0);
int size = maxRight.size();
// 记录每个柱子左边柱子最大高度
maxLeft[0] = height[0];
for (int i = 1; i < size; i++) {
maxLeft[i] = max(height[i], maxLeft[i - 1]);
}
// 记录每个柱子右边柱子最大高度
maxRight[size - 1] = height[size - 1];
for (int i = size - 2; i >= 0; i--) {
maxRight[i] = max(height[i], maxRight[i + 1]);
}
// 求和
int sum = 0;
for (int i = 0; i < size; i++) {
int count = min(maxLeft[i], maxRight[i]) - height[i];
if (count > 0) sum += count;
}
return sum;
}
};
单调栈解法:
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() <= 2) return 0; // 可以不加
stack<int> st; // 存着下标,计算的时候用下标对应的柱子高度
st.push(0);
int sum = 0;
for (int i = 1; i < height.size(); i++) {
if (height[i] < height[st.top()]) { // 情况一
st.push(i);
} if (height[i] == height[st.top()]) { // 情况二
st.pop(); // 其实这一句可以不加,效果是一样的,但处理相同的情况的思路却变了。
st.push(i);
} else { // 情况三
while (!st.empty() && height[i] > height[st.top()]) { // 注意这里是while
int mid = st.top();
st.pop();
if (!st.empty()) {
int h = min(height[st.top()], height[i]) - height[mid];
int w = i - st.top() - 1; // 注意减一,只求中间宽度
sum += h * w;
}
}
st.push(i);
}
}
return sum;
}
};
84.柱状图中最大的矩形
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
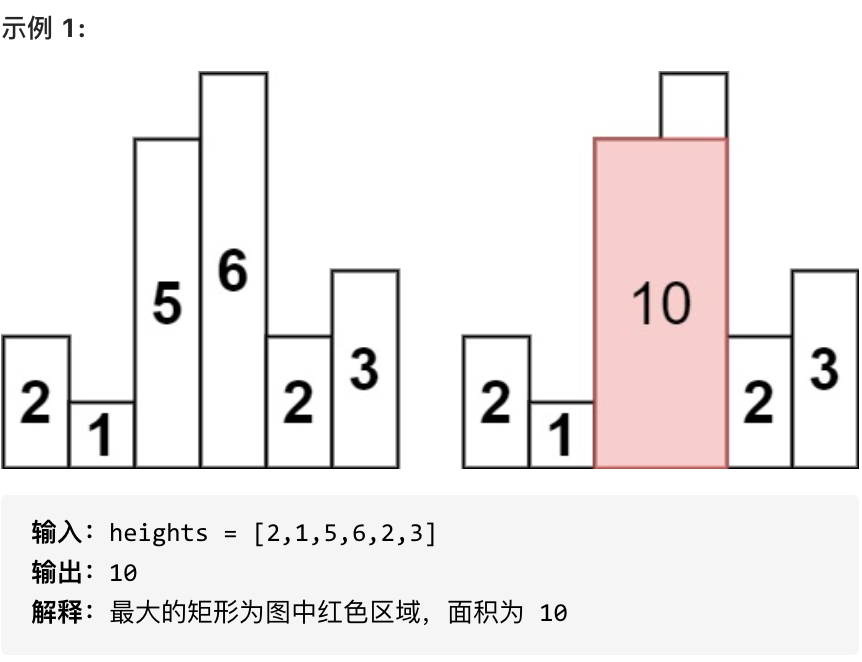
双指针法:超时
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
int sum = 0;
for (int i = 0; i < heights.size(); i++) {
int left = i;
int right = i;
for (; left >= 0; left--) {
if (heights[left] < heights[i]) break;
}
for (; right < heights.size(); right++) {
if (heights[right] < heights[i]) break;
}
int w = right - left - 1;
int h = heights[i];
sum = max(sum, w * h);
}
return sum;
}
};
动态规划:
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
vector<int> minLeftIndex(heights.size());
vector<int> minRightIndex(heights.size());
int size = heights.size();
// 记录每个柱子 左边第一个小于该柱子的下标
minLeftIndex[0] = -1; // 注意这里初始化,防止下面while死循环
for (int i = 1; i < size; i++) {
int t = i - 1;
// 这里不是用if,而是不断向左寻找的过程
while (t >= 0 && heights[t] >= heights[i]) t = minLeftIndex[t];
minLeftIndex[i] = t;
}
// 记录每个柱子 右边第一个小于该柱子的下标
minRightIndex[size - 1] = size; // 注意这里初始化,防止下面while死循环
for (int i = size - 2; i >= 0; i--) {
int t = i + 1;
// 这里不是用if,而是不断向右寻找的过程
while (t < size && heights[t] >= heights[i]) t = minRightIndex[t];
minRightIndex[i] = t;
}
// 求和
int result = 0;
for (int i = 0; i < size; i++) {
int sum = heights[i] * (minRightIndex[i] - minLeftIndex[i] - 1);
result = max(sum, result);
}
return result;
}
};
单调栈:
// 版本一
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
heights.insert(heights.begin(), 0); // 数组头部加入元素0
heights.push_back(0); // 数组尾部加入元素0
st.push(0);
int result = 0;
// 第一个元素已经入栈,从下标1开始
for (int i = 1; i < heights.size(); i++) {
// 注意heights[i] 是和heights[st.top()] 比较 ,st.top()是下标
if (heights[i] > heights[st.top()]) {
st.push(i);
} else if (heights[i] == heights[st.top()]) {
st.pop(); // 这个可以加,可以不加,效果一样,思路不同
st.push(i);
} else {
while (heights[i] < heights[st.top()]) { // 注意是while
int mid = st.top();
st.pop();
int left = st.top();
int right = i;
int w = right - left - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
}
return result;
}
};
代码精简之后:
// 版本二
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
stack<int> st;
heights.insert(heights.begin(), 0); // 数组头部加入元素0
heights.push_back(0); // 数组尾部加入元素0
st.push(0);
int result = 0;
for (int i = 1; i < heights.size(); i++) {
while (heights[i] < heights[st.top()]) {
int mid = st.top();
st.pop();
int w = i - st.top() - 1;
int h = heights[mid];
result = max(result, w * h);
}
st.push(i);
}
return result;
}
};




