HJ46 截取字符串

约 6666 字大约 22 分钟...

HJ46 截取字符串

描述

输入一个字符串和一个整数 k ，截取字符串的前k个字符并输出

数据范围：字符串长度满足 1≤n≤1000  ， 1≤k≤n

输入描述：

1.输入待截取的字符串

2.输入一个正整数k，代表截取的长度

输出描述：

截取后的字符串

方法一：substr（）

#include <iostream>
#include <string>

using namespace std;

int main()
{
    string str;
    int k;
    while(cin>>str>>k){//输入字符串和k
        string sub_str = str.substr(0,k);
        cout<<sub_str<<endl;//输出前k个字符
    }
}
点击并拖拽以移动

方法二：遍历

#include <iostream>
#include <string>

using namespace std;

int main()
{
    string str;
    int k;
    while(cin>>str>>k){//输入字符串和k
        for(int i = 0;i < k;i++){//遍历一遍字符串，输出前k个字符
            cout<<str[i];
        }
        cout<<endl;
    }
}
点击并拖拽以移动

HJ48 从单向链表中删除指定值的节点

方法一：数组模拟

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

int main(){
    int n, head;
    while(cin >> n >> head){
        vector<int> array; //用数组模拟链表
        array.push_back(head);
        for(int i = 1; i < n; i++){
            int num, pos_num;
            cin >> num >> pos_num; //输入要插入的数和它要插入哪个数字后面
            auto iter = find(array.begin(), array.end(), pos_num); //找到要插入后面你的那个位置
            if(iter == array.end()) //结尾push_back
                array.push_back(num);
            else //中间insert
                array.insert(iter + 1, num);
        }
        int remove;
        cin >> remove;
        array.erase(find(array.begin(), array.end(), remove)); //找到要移除的数字的位置
        for(int i = 0; i < array.size(); i++) //输出
            cout << array[i] << " ";
        cout << endl;
    }
    return 0;
}
点击并拖拽以移动

方法二：链表

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

struct node{ //链表结点
    int val;
    struct node* next = NULL;
};

int main(){
    int n, val;
    while(cin >> n >> val){
        node* head = new node; //头结点
        head->val = val;
        for(int i = 1; i < n; i++){
            int pre, cur;
            cin >> cur >> pre;
            node* p = new node; //添加这个结点
            p->val = cur;
            node* q = head;
            while(q->val != pre) //找到前序结点
                q = q->next;
            p->next = q->next; //断开
            q->next = p; //插入
        }
        int remove;
        cin >> remove;
        node* p = head;
        while(p != NULL){
            if(p->val != remove) //不输出remove，其他都输出
                cout << p->val << " ";
            p = p->next;
        }
        cout << endl;
    }
    return 0;
}
点击并拖拽以移动

HJ50 四则运算

描述

输入一个表达式（用字符串表示），求这个表达式的值。

保证字符串中的有效字符包括[‘0’-‘9’],‘+’,‘-’, ‘*’,‘/’ ,‘(’， ‘)’,‘[’, ‘]’,‘{’ ,‘}’。且表达式一定合法。

数据范围：表达式计算结果和过程中满足 ∣val∣≤1000  ，字符串长度满足 1≤n≤1000

输入描述：

输入一个算术表达式

输出描述：

得到计算结果

方法一：递归

#include<iostream>
#include<string>
#include<vector>
using namespace std;

int compute(string& s, int left, int right){
    char op = '+'; //默认加开始
    int num = 0;
    vector<int> st;
    for(int i = left; i <= right; i++){
        if(isdigit(s[i])) //数字
            num = num * 10 + s[i] - '0'; //计算该部分数字总和
        if(s[i] == '{' || s[i] == '[' || s[i] == '('){ //进入左括号
            int layer = 0; //统计左括号层数
            int j = i;
            while(j <= right){ //遍历到右边
                if(s[j] == '{' || s[j] == '[' || s[j] == '(')
                    layer++; //遇到左括号，层数累加
                else if(s[j] == '}' || s[j] == ']' || s[j] == ')'){
                    layer--; //遇到右括号层数递减
                    if(layer == 0) //直到层数为0
                        break;
                }
                j++;
            }
            num = compute(s, i + 1, j - 1); //递归计算括号中的部分
            i = j + 1;
        }
        if(!isdigit(s[i]) || i == right){ //遇到运算符或者结尾
            switch(op){ //根据运算符开始计算
                case '+': st.push_back(num); break; //加减法加入到末尾
                case '-': st.push_back(-num); break;
                case '*': st.back() *= num; break; //乘除法与末尾计算
                case '/': st.back() /= num; break;
            }
            op = s[i]; //修改为下一次的运算符
            num = 0;
        }
    }
    int res = 0; 
    for(int x : st) //累加和
        res += x;
    return res;
}
int main(){
    string s;
    while(cin >> s){
        cout << compute(s, 0, s.length() - 1) << endl;
    }
    return 0;
}
点击并拖拽以移动

方法二：双栈法

​

点击并拖拽以移动
#include<iostream>
#include<stack>
using namespace std;

void compute(stack<int>& st1, stack<char>& st2){ //根据栈顶运算符弹出栈顶两个元素进行运算
    int b = st1.top();
        st1.pop();
    int a = st1.top();
        st1.pop();
    char op = st2.top(); //栈顶运算符
        st2.pop();
    if(op == '+') a = a + b; //加
    else if(op == '-') a = a - b; //减
    else if(op == '*') a = a * b; //乘
    else if(op == '/') a = a / b; //除
    st1.push(a);
}

bool priority(char m, char n){ //比较运算符优先级
    if(m == '(') //括号优先级最高
        return false;
    else if((m == '+' || m == '-') && (n == '*' || n == '/')) //加减法小于乘除法
        return false;
    return true;
}
int main(){
    string s;
    while(cin >> s){
       stack<int> st1; //记录运算数字
       stack<char> st2; //记录运算符
       st2.push('('); //整个运算式添加括号
       s += ')';
       bool flag = false;
       for(int i = 0; i < s.length(); i++){
           if(s[i] == '(' || s[i] == '[' || s[i] == '{') //如果是左括号都在运算符栈加入(
               st2.push('(');
           else if(s[i] == ')' || s[i] == ']' || s[i] == '}'){ //遇到右括号
               while(st2.top() != '('){ //弹出开始计算直到遇到左括号
                   compute(st1, st2);
               }
               st2.pop(); //弹出左括号
           } else if(flag){ //运算符
               while(priority(st2.top(), s[i])){ //比较运算优先级
                   compute(st1, st2); //可以直接计算
               }
               st2.push(s[i]); //需要将现阶段加入栈中等待运算
               flag = false;
           } else{ //数字
                int j = i; //记录起始
                if(s[j] == '-' || s[j] == '+') //正负号
                    i++;
                while(isdigit(s[i])){
                    i++;
                }
                string temp = s.substr(j, i - j); 
                st1.push(stoi(temp)); //截取数字部分，转数字
                i--;
                flag = true; //数字结束，下一次flag为true就是运算符了
           }
       }
      cout << st1.top() << endl; //输出
    }
    return 0;
}
点击并拖拽以移动

HJ51 输出单向链表中倒数第k个结点

描述

输入一个单向链表，输出该链表中倒数第k个结点，链表的倒数第1个结点为链表的尾指针。

链表结点定义如下：

struct ListNode {     int m_nKey;     ListNode* m_pNext; };

正常返回倒数第k个结点指针，异常返回空指针.

要求：

(1)正序构建链表;

(2)构建后要忘记链表长度。

数据范围：链表长度满足 1≤n≤1000  ，k≤n  ，链表中数据满足0≤val≤10000

本题有多组样例输入。

输入描述：

输入说明
1 输入链表结点个数
2 输入链表的值
3 输入k的值

输出描述：

输出一个整数

方法一：根据长度找倒数k

#include<iostream>
using namespace std;

struct ListNode{ //链表结点
    int val;
    ListNode* next;
    ListNode(int x) : val(x), next(NULL){} //初始化
};
ListNode* FindKthToTail(ListNode* pHead, int k, int n) { //找到链表倒数第k个结点
    ListNode* p = pHead;
    if(n < k) //长度过小，返回空链表
        return p = NULL;
    for(int i = 0; i < n - k; i++) //遍历n-k次
        p = p->next;
    return p;
}

int main(){
    int n;
    while(cin >> n){ //输入n
        int val;
        cin >> val;
        ListNode *head = new ListNode(val); //链表第一个结点
        ListNode *p = head;
        for(int i = 1; i < n; i++){ //输入链表后续结点
            cin >> val;
            ListNode *q = new ListNode(val);
            p->next = q; //连接
            p = p->next;
        }
        int k;
        cin >> k; //输入k
        if(k == 0) //k等于0直接输出0
            cout << 0 << endl;
        else{
            p = FindKthToTail(head, k, n); //找到第k个结点
            if(p != NULL) //返回不为null才能输出
                cout << p->val << endl;
        }
    }
    return 0;
}
点击并拖拽以移动

方法二：快慢双指针

​ 

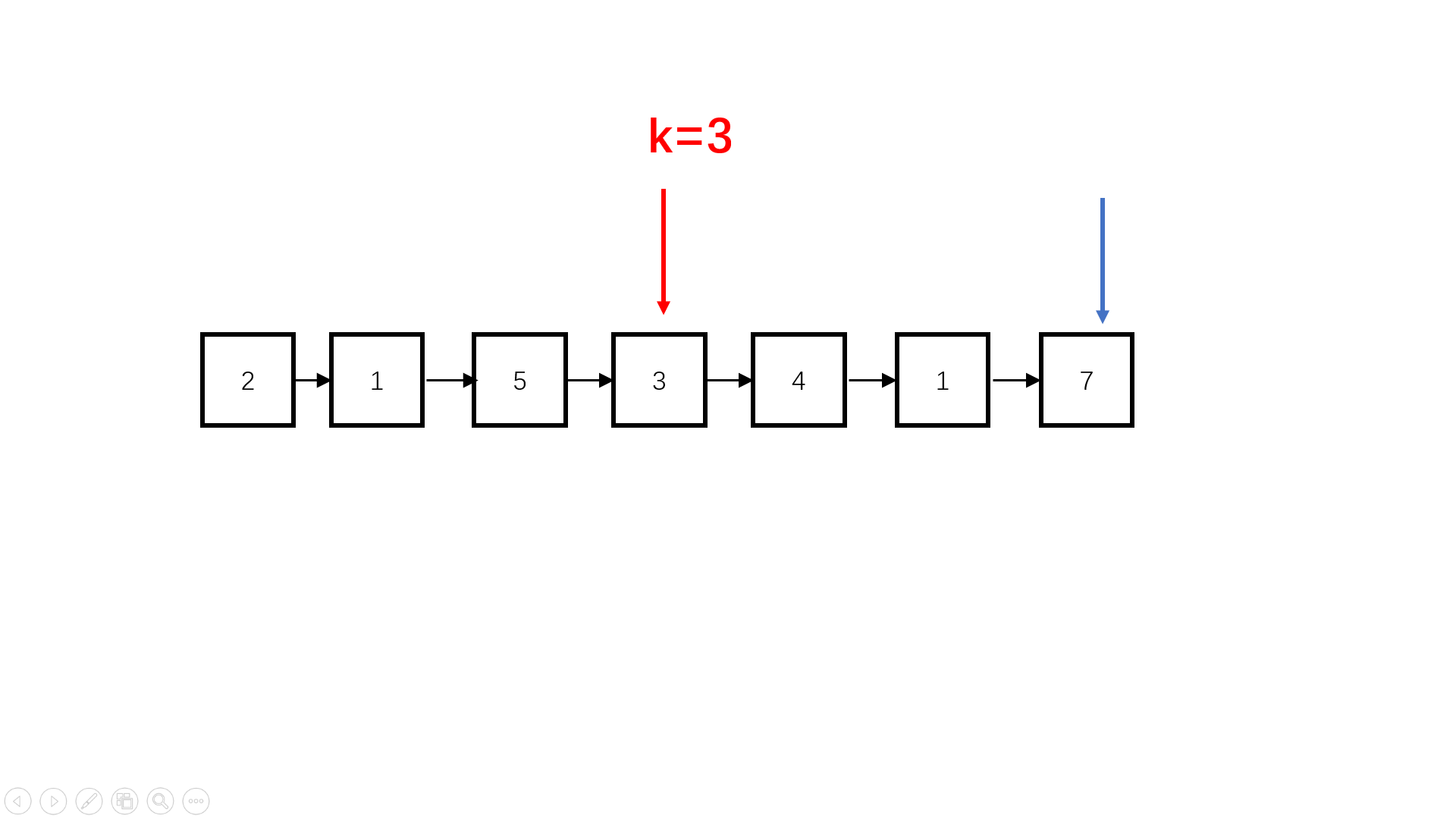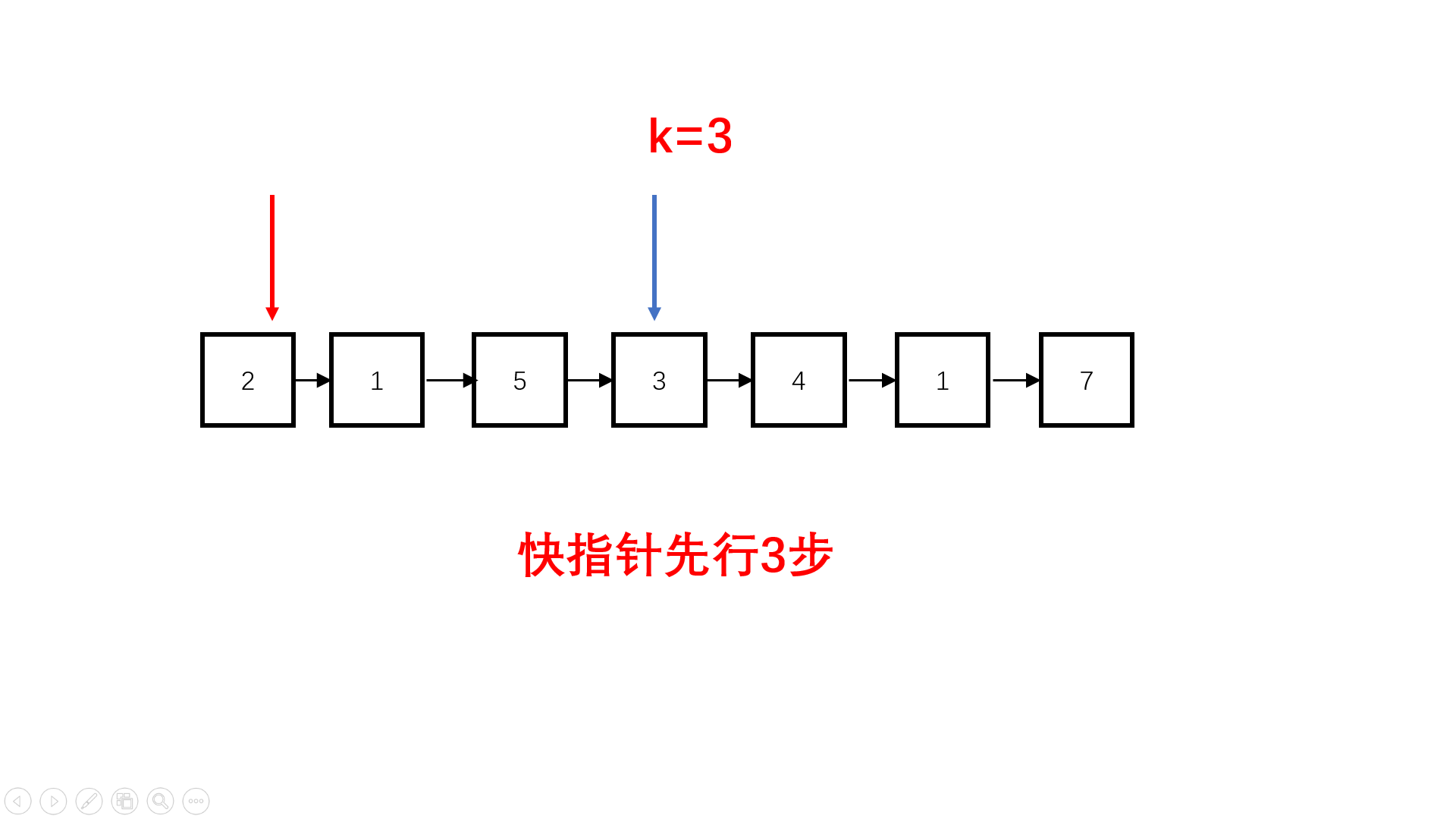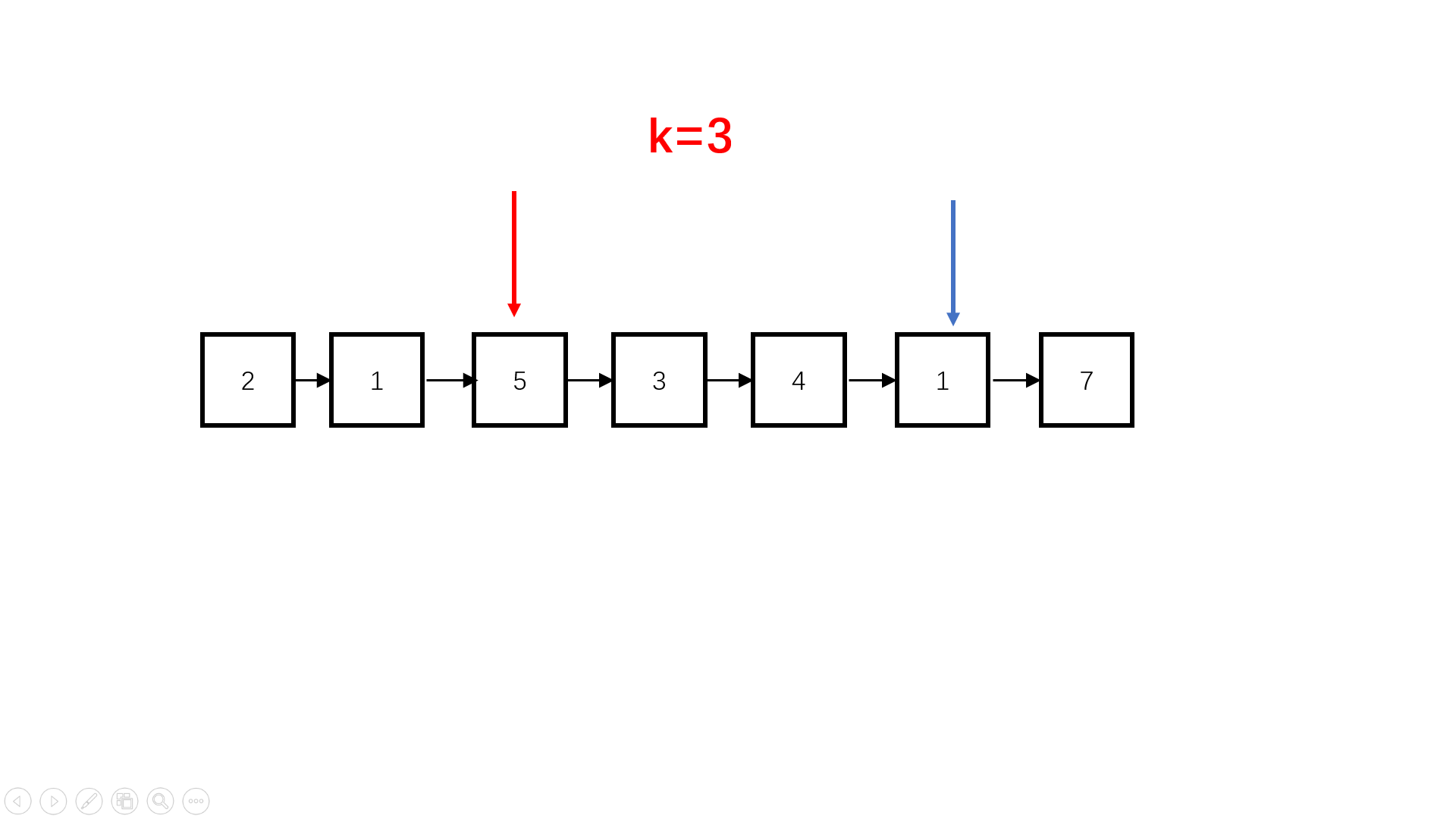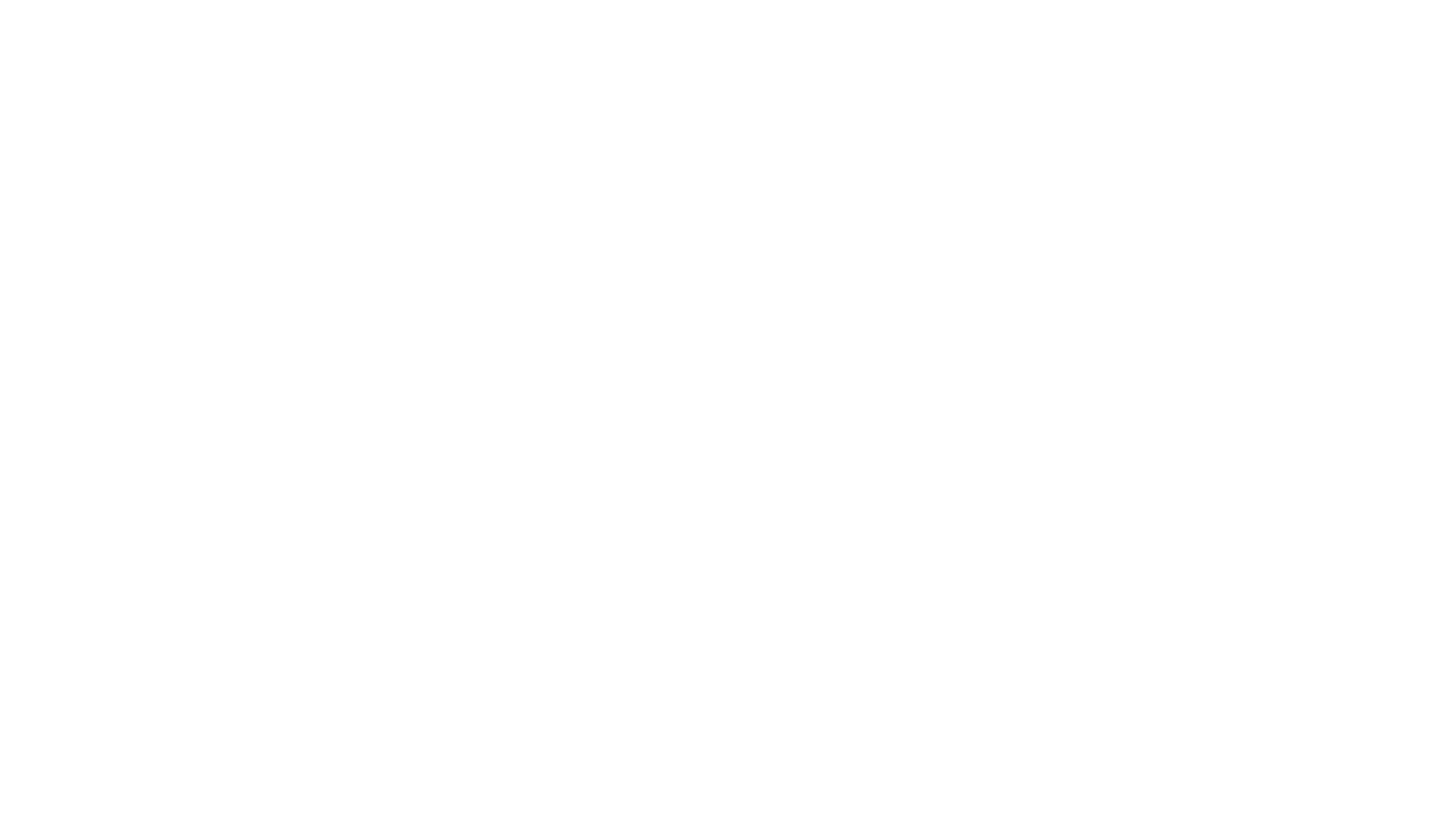
#include<iostream>
using namespace std;

struct ListNode{ //链表结点
    int val;
    ListNode* next;
    ListNode(int x) : val(x), next(NULL){} //初始化
};
ListNode* FindKthToTail(ListNode* pHead, int k) {//找到链表倒数第k个结点
    int n = 0;
    ListNode* fast = pHead;
    ListNode* slow = pHead;
    for(int i = 0; i < k; i++){  //快指针先行k步
        if(fast != NULL)
            fast = fast->next;
        else //达不到k步说明链表过短，返回空链表
            return slow = NULL;
    }
    while(fast != NULL){ //快慢指针同步，快指针先到底，慢指针指向倒数第k个
        fast = fast->next;
        slow = slow->next;
    }
    return slow;
}

int main(){
    int n;
    while(cin >> n){ //输入n
        int val;
        cin >> val;
        ListNode *head = new ListNode(val); //链表第一个结点
        ListNode *p = head;
        for(int i = 1; i < n; i++){ //输入链表后续结点
            cin >> val;
            ListNode *q = new ListNode(val);
            p->next = q; //连接
            p = p->next;
        }
        int k;
        cin >> k; //输入k
        if(k == 0) //k等于0直接输出0
            cout << 0 << endl;
        else{
            p = FindKthToTail(head, k); //找到第k个结点
            if(p != NULL) //返回不为null才能输出
                cout << p->val << endl;
        }
    }
    return 0;
}

​

HJ52 计算字符串的编辑距离

描述

Levenshtein 距离，又称编辑距离，指的是两个字符串之间，由一个转换成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。编辑距离的算法是首先由俄国科学家 Levenshtein 提出的，故又叫 Levenshtein Distance 。

例如：

字符串A: abcdefg

字符串B: abcdef

通过增加或是删掉字符 ”g” 的方式达到目的。这两种方案都需要一次操作。把这个操作所需要的次数定义为两个字符串的距离。

要求：

给定任意两个字符串，写出一个算法计算它们的编辑距离。

数据范围：给定的字符串长度满足 1≤len(str)≤1000

输入描述：

每组用例一共2行，为输入的两个字符串

输出描述：

每组用例输出一行，代表字符串的距离

方法一：动态规划

​

点击并拖拽以移动
#include<iostream>
#include<string>
#include<vector>
#include<algorithm>

using namespace std;

int main() {
    string str1, str2;
    while (cin >> str1 >> str2) {
        vector<vector<int>> dp(str1.size() + 1, vector<int>(str2.size() + 1, 0));
        for (int i = 1; i <= str2.size(); i++) dp[0][i] = i;//str1从0个字符变成str2的i个字符需要i个插入操作
        for (int i = 1; i <= str1.size(); i++) dp[i][0] = i;//str1从i个字符变成str2的0个字符也需要i个删除操作
        for(int i=1;i<=str1.size();i++){
            for (int j = 1; j <= str2.size(); j++) {
                int op1 = dp[i-1][j] + 1;//删除字符str1[i-1]
                int op2 = dp[i][j-1] + 1;//删除字符str2[j-1]
                int op3 = dp[i-1][j-1];//替换操作
                if(str1[i-1] != str2[j-1]){
                    op3++;
                }
                dp[i][j] = min(min(op1, op2), op3);//替换操作和删除操作取最小
            }
        }
        cout << dp[str1.size()][str2.size()] << endl;
    }
}
点击并拖拽以移动

方法二：滚动数组+动态规划

#include<iostream>
#include<string>
#include<vector>
#include<algorithm>

using namespace std;

int main() {
    string str1, str2;
    while (cin >> str1 >> str2) {
        vector<int> dp(str2.size() + 1, 0);
        for(int i = 0; i <= str2.size(); i++)//初始化第一行
            dp[i] = i;
        for(int i = 1; i <= str1.size(); i++){
            dp[0] = i;//初始化dp[0]，i->0需要i个删除操作
            int l = dp[0] - 1;
            for (int j = 1; j <= str2.size(); j++) {
                int curr = dp[j];//保留当前的值，作为dp[j+1]的左上角值
                dp[j] = min(min(dp[j] + 1, dp[j-1] + 1), ((str1[i-1] == str2[j-1])?0:1) + l);
                l = curr;//更新左上角值
            }
        }
        cout << dp[str2.size()]<< endl;
    }
}
点击并拖拽以移动

HJ53 杨辉三角的变形

描述

​

点击并拖拽以移动

以上三角形的数阵，第一行只有一个数1，以下每行的每个数，是恰好是它上面的数、左上角数和右上角的数，3个数之和（如果不存在某个数，认为该数就是0）。

求第n行第一个偶数出现的位置。如果没有偶数，则输出-1。例如输入3,则输出2，输入4则输出3，输入2则输出-1。

数据范围： 1≤n≤109

输入描述：

输入一个int整数

输出描述：

输出返回的int值

方法一：数组模拟（超出空间）

​

点击并拖拽以移动
#include<iostream>
#include<vector>
using namespace std;

int main(){
    int n;
    while(cin >> n){
        vector<vector<int> > matrix(n, vector<int>(2 * n - 1, 0)); //一共n行，最下面一行最多有2*n-1个元素
        matrix[0][n - 1] = 1; //顶角
        matrix[n - 1][0] = matrix[n - 1][2 * n - 2] = 1; //两个底角
        for(int i = 1; i < n; i++)
            for(int j = 1; j < 2 * n - 2; j++)
                matrix[i][j] = matrix[i - 1][j - 1] + matrix[i - 1][j] + matrix[i - 1][j + 1];
        for(int i = 0; i < 2 * n - 1; i++){
            if(matrix[n - 1][i] != 0 && matrix[n - 1][i] % 2 == 0){ //非0偶数
                cout << i + 1 << endl; //输出下标加1;
                break;
            }
            if(i >= n - 1 && matrix[n - 1][i] == 1){ //过一半还没有找到偶数且遇到了1代表永远找不到了
                cout << -1 << endl;
                break;
            }
        }
    }
    return 0;
}
点击并拖拽以移动

方法二：数学规律

​

点击并拖拽以移动
#include<iostream>
using namespace std;

int main(){
    int n;
    while(cin >> n){
        if(n <= 2) //小于等于2的行没有偶数
            cout << -1 << endl;
        else{
            if(n % 2) //奇数行偶数在第2个
                cout << 2 << endl;
            else if(n % 4 == 2) //偶数除4余2的在第4个
                cout << 4 << endl;
            else if(n % 4 == 0) //整除4的在第3个
                cout << 3 << endl;
        }
    }
    return 0;
}
点击并拖拽以移动

HJ54 表达式求值

描述

给定一个字符串描述的算术表达式，计算出结果值。

输入字符串长度不超过 100 ，合法的字符包括 ”+, -, *, /, (, )” ， ”0-9” 。

数据范围：运算过程中和最终结果均满足∣val∣≤2^31−1  ，即只进行整型运算，确保输入的表达式合法

输入描述：

输入算术表达式

输出描述：

计算出结果值

方法一：递归

#include<iostream>
#include<string>
#include<vector>
using namespace std;

int compute(string& s, int left, int right){
    char op = '+'; //默认加开始
    int num = 0;
    vector<int> st;
    for(int i = left; i <= right; i++){
        if(isdigit(s[i])) //数字
            num = num * 10 + s[i] - '0'; //计算该部分数字总和
        if(s[i] == '('){ //进入左括号
            int layer = 0; //统计左括号层数
            int j = i;
            while(j <= right){ //遍历到右边
                if(s[j] == '(')
                    layer++; //遇到左括号，层数累加
                else if(s[j] == ')'){
                    layer--; //遇到右括号层数递减
                    if(layer == 0) //直到层数为0
                        break;
                }
                j++;
            }
            num = compute(s, i + 1, j - 1); //递归计算括号中的部分
            i = j + 1;
        }
        if(!isdigit(s[i]) || i == right){ //遇到运算符或者结尾
            switch(op){ //根据运算符开始计算
                case '+': st.push_back(num); break; //加减法加入到末尾
                case '-': st.push_back(-num); break;
                case '*': st.back() *= num; break; //乘除法与末尾计算
                case '/': st.back() /= num; break;
            }
            op = s[i]; //修改为下一次的运算符
            num = 0;
        }
    }
    int res = 0; 
    for(int x : st) //累加和
        res += x;
    return res;
}
int main(){
    string s;
    while(cin >> s){
        cout << compute(s, 0, s.length() - 1) << endl;
    }
    return 0;
}
点击并拖拽以移动

方法二：双栈法

​

点击并拖拽以移动
#include<iostream>
#include<stack>
using namespace std;

void compute(stack<int>& st1, stack<char>& st2){ //根据栈顶运算符弹出栈顶两个元素进行运算
    int b = st1.top();
        st1.pop();
    int a = st1.top();
        st1.pop();
    char op = st2.top(); //栈顶运算符
        st2.pop();
    if(op == '+') a = a + b; //加
    else if(op == '-') a = a - b; //减
    else if(op == '*') a = a * b; //乘
    else if(op == '/') a = a / b; //除
    st1.push(a);
}

bool priority(char m, char n){ //比较运算符优先级
    if(m == '(') //括号优先级最高
        return false;
    else if((m == '+' || m == '-') && (n == '*' || n == '/')) //加减法小于乘除法
        return false;
    return true;
}
int main(){
    string s;
    while(cin >> s){
       stack<int> st1; //记录运算数字
       stack<char> st2; //记录运算符
       st2.push('('); //整个运算式添加括号
       s += ')';
       bool flag = false;
       for(int i = 0; i < s.length(); i++){
           if(s[i] == '(') //如果是左括号都在运算符栈加入(
               st2.push('(');
           else if(s[i] == ')'){ //遇到右括号
               while(st2.top() != '('){ //弹出开始计算直到遇到左括号
                   compute(st1, st2);
               }
               st2.pop(); //弹出左括号
           } else if(flag){ //运算符
               while(priority(st2.top(), s[i])){ //比较运算优先级
                   compute(st1, st2); //可以直接计算
               }
               st2.push(s[i]); //需要将现阶段加入栈中等待运算
               flag = false;
           } else{ //数字
                int j = i; //记录起始
                if(s[j] == '-' || s[j] == '+') //正负号
                    i++;
                while(isdigit(s[i])){
                    i++;
                }
                string temp = s.substr(j, i - j); 
                st1.push(stoi(temp)); //截取数字部分，转数字
                i--;
                flag = true; //数字结束，下一次flag为true就是运算符了
           }
       }
      cout << st1.top() << endl; //输出
    }
    return 0;
}
点击并拖拽以移动

HJ55 挑7

描述

输出 1到n之间 的与 7 有关数字的个数。

一个数与7有关是指这个数是 7 的倍数，或者是包含 7 的数字（如 17 ，27 ，37 ... 70 ，71 ，72 ，73...）

数据范围：1≤n≤30000

输入描述：

一个正整数 n 。( n 不大于 30000 )

输出描述：

一个整数，表示1到n之间的与7有关的数字个数。

方法一：连除法判断

​

点击并拖拽以移动
#include<iostream>
using namespace std;

bool select7(int i){
    if(i % 7 == 0) //7的倍数
        return true;
    while(i != 0){ //连除法
        if(i % 10 == 7) //数字里包含7
            return true;
        i /= 10;
    }
    return false;
}
int main(){
    int n;
    while(cin >> n){
        int count = 0;
        for(int i = 1; i <= n; i++) //穷举1到n
            if(select7(i)) //查看是否符合要求
                count++;
        cout << count << endl;
    }
    return 0;
}
点击并拖拽以移动
#include<iostream>
#include<string>
using namespace std;

int main(){
    int n;
    while(cin >> n){
        int count = 0;
        for(int i = 7; i <= n; i++) //枚举7到n
            if(i % 7 == 0 || to_string(i).find('7', 0) != string::npos) //整除7或者转化字符串后能找到字符7
                count++;
        cout << count << endl;
    }
    return 0;
}
点击并拖拽以移动

HJ56 完全数计算

描述

完全数（Perfect number），又称完美数或完备数，是一些特殊的自然数。

它所有的真因子（即除了自身以外的约数）的和（即因子函数），恰好等于它本身。

例如：28，它有约数1、2、4、7、14、28，除去它本身28外，其余5个数相加，1+2+4+7+14=28。

输入n，请输出n以内(含n)完全数的个数。

数据范围：1≤n≤5×105

输入描述：

输入一个数字n

输出描述：

输出不超过n的完全数的个数

方法一：

大数学家欧拉曾推算出完全数的获得公式：如果p是质数，且2p-1也是质数，那么（2p-1）X2^（p-1）便是一个完全数。
例如p=2，是一个质数，2p-1=3也是质数，（2p-1）X2^（p-1）=3X2=6，是完全数。
例如p=3，是一个质数，2p-1=7也是质数，（2p-1）X2^（p-1）=7X4=28，是完全数。
例如p=5，是一个质数，2p-1=31也是质数，（2p-1）X2^（p-1）=31X16=496是完全数。
当2^p-1是质数的时候，称其为梅森素数。到2013年2月6日为止，人类只发现了48个梅森素数，较小的有3、7、31、127等

//C++
#include <iostream>
#include <math.h>

using namespace std;

bool is_prime(int p);

// 如果p是质数，且2^p-1也是质数，那么（2^p-1）X2^（p-1）便是一个完全数
int main()
{
    int n;
    while(cin >> n)
    {
        int count = 0;
        for(int p=2; p<sqrt(n); p++)
        {
            long int t = pow(2,p)-1;
            if( is_prime(p) && is_prime(t) )
            {
                int perfect_num = pow(2,p-1) * t;
                if(  perfect_num>0 && perfect_num<n )
                    count++;
            }     
        }
        cout << count << endl;
    }
    return 0;
}

bool is_prime(int p)
{
    for(int i=2; i<sqrt(p); i++)
        if(p % i == 0)
            return false;
    return true;
}
点击并拖拽以移动

方法二：

#include <bits/stdc++.h>
using namespace std;

int main()
{

    int n;  //待输入的数
    while(cin>>n){
        int count=0;  //计数器
        //遍历从2到n的每一个数，并在下一层for计算是否为完全数
        for(int k=2;k<=n;k++)  
        {
            int sum=1;  //每个数都包含1这个因数
            for(int i=2;i<=k/2;i++) //除以2：根据题干推出的缩小i范围的方法
            {
                if(k%i==0)
                    sum=sum+i;
            }
            if(k==sum)
                count++;
        }
        cout<<count<<endl;
    }
    return 0;
}
点击并拖拽以移动

HJ57 高精度整数加法

描述

输入两个用字符串 str 表示的整数，求它们所表示的数之和。

数据范围： 1≤len(str)≤10000

输入描述：

输入两个字符串。保证字符串只含有'0'~'9'字符

输出描述：

输出求和后的结果

方法一：

#include<iostream>
#include<string>
#include<stack>
#include<algorithm>
using namespace std;

// 将两个字符串扔到两个栈中，逐个斩当头，直到两个栈都空
// 主要是注意进位问题，最后一位的问题
int main() {
    string s1, s2;
    while (cin >> s1 >> s2) {
        string ans;
        stack<char> st1;
        stack<char> st2;
        for (char c : s1) {
            st1.push(c);
        }
        for (char c : s2) {
            st2.push(c);
        }
        int flag = 0;
        while (st1.size() != 0 || st2.size() != 0) {
            int temp = 0;
            if (st1.size() != 0) {
                temp += st1.top() - '0';
                st1.pop();
            }
            if (st2.size() != 0) {
                temp += st2.top() - '0';
                st2.pop();
            }
            // temp和flag加完后再取余和除以，这是考虑到加完flag后刚好为10的情况
            ans += (temp + flag) % 10 + '0';
            flag = (temp + flag) / 10;
            // 对于两个栈都空之前，判断有没有进位，如果进位则直接加'1'
            if (flag == 1 && st1.size() == 0 && st2.size() ==0)
                ans += '1';
        }
        // 记得反转一下再输出
        reverse(ans.begin(), ans.end());
        cout << ans << endl;

    }


    return 0;
}
点击并拖拽以移动

HJ58 输入n个整数，输出其中最小的k个

描述

输入n个整数，找出其中最小的k个整数并按升序输出

本题有多组输入样例

数据范围：1≤n≤1000  ，输入的整数满足 1≤val≤10000

输入描述：

第一行输入两个整数n和k
第二行输入一个整数数组

输出描述：

从小到大输出最小的k个整数，用空格分开

方法一：暴力方法

​

点击并拖拽以移动
#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,k;
    while(cin>>n>>k)
    {   //输入n和k
        vector<int> num;
        for(int i=0;i<n;i++)
        {   //逐个储存n个整数
            int temp;
            cin>>temp;
            num.push_back(temp);
        }
        sort(num.begin(),num.end());//对n个数进行升序排序
        for(int i=0;i<k-1;i++)
        {   //输出前k个数字
            cout<<num[i]<<' ';
        }
        cout<<num[k-1]<<endl;//最后一个数字输出后不要输出空格了
    }
    return 0;
}
点击并拖拽以移动

方法二：堆方法

​

点击并拖拽以移动
#include <bits/stdc++.h>
using namespace std;
int main()
{
    int n = 0, k = 0;
    while(cin >> n >> k)
    {
        vector<int> vec;
        int num = 0;
        while(n--)
        {
            cin >> num;
            vec.push_back(num);
        }
        //建堆k*logk
        vector<int> heap(vec.begin(), vec.begin() + k);
        make_heap(heap.begin(), heap.end(), less<int>());
        //插入(n - k)*logk
        for(int i = k; i < vec.size(); i++)
        {
            if(vec[i] < heap[0])
            {
                //插入一个更小的
                heap.push_back(vec[i]);
                push_heap(heap.begin(), heap.end());
                //弹出一个最大的
                pop_heap(heap.begin(), heap.end());
                heap.pop_back();
            }
        }
        //从小到大输出,k*logk + k
        sort(heap.begin(), heap.end());
        for(int i = 0; i < heap.size(); i++)
        {
            cout << heap[i];
            if(i != heap.size() - 1)
            {
                cout << " ";
            }
        }
        cout << endl;
    }
}
点击并拖拽以移动

HJ59 找出字符串中第一个只出现一次的字符

描述

找出字符串中第一个只出现一次的字符

数据范围：输入的字符串长度满足1≤n≤1000

输入描述：

输入一个非空字符串

输出描述：

输出第一个只出现一次的字符，如果不存在输出-1

方法一：哈希表统计频率

#include<iostream>
#include<string>
#include<unordered_map>
using namespace std;

int firstNotRepeat(string& str) {
    unordered_map<char, int> mp;
    for(int i = 0; i < str.length(); i++) //统计每个字符出现的次数
        mp[str[i]]++;
    for(int i = 0; i < str.length(); i++) //找到第一个只出现一次的字母
        if(mp[str[i]] == 1)
           return i;
    return -1; //没有找到
}

int main(){
    string s;
    while(getline(cin, s)){ 
        int pos = firstNotRepeat(s); //找到该该字符的位置
        if(pos == -1) //没找到输出-1
            cout << -1 << endl;
        else
            cout << s[pos] << endl; //输出字符
    }
    return 0;
}
点击并拖拽以移动

方法二：队列+哈希表统计位置

​

点击并拖拽以移动
#include<iostream>
#include<string>
#include<unordered_map>
#include<queue>
using namespace std;

int firstNotRepeat(string& str) {
    unordered_map<char, int> mp; //统计字符出现的位置
    queue<pair<char, int> > q;
    for(int i = 0; i < str.length(); i++){
        if(!mp.count(str[i])){ //没有出现过的字符
            mp[str[i]] = i;
            q.push(make_pair(str[i], i));
        }else{ //找到重复的字符
            mp[str[i]] = -1; //位置置为-1
            while(!q.empty() && mp[q.front().first] == -1) //弹出前面所有的重复过的字符
                q.pop();
        }
    }
    return q.empty() ? -1 : q.front().second;
 }

int main(){
    string s;
    while(getline(cin, s)){ 
        int pos = firstNotRepeat(s); //找到该该字符的位置
        if(pos == -1) //没找到输出-1
            cout << -1 << endl;
        else
            cout << s[pos] << endl; //输出字符
    }
    return 0;
}
点击并拖拽以移动

方法三：首次末次比较解法

​

点击并拖拽以移动
#include <bits/stdc++.h>
using namespace std;
int main()
{
    string str;
    while(cin >> str)
    {
        bool flag = false;//flag用来判断是否存在只出现一次的字符
        for(int i =0;i<str.size();i++)//遍历一遍字符串
        {
            if(str.find_first_of(str[i]) == str.find_last_of(str[i]))//判断当前字符是否是只出现了一次
            {
                cout << str[i] << endl;//若是，则输出这个字符
                flag = true;
                break;//找到了第一次出现的字符，跳出循环
            }
        }
        if(!flag) cout << "-1" << endl;//如果没有找到第一次出现的字符，则输出-1
    }
    return 0;
}
点击并拖拽以移动

方法四：频数统计方法

​

点击并拖拽以移动
#include <bits/stdc++.h>
using namespace std;
int main()
{
    string str;
    while(cin>>str)
    {
        int count[26] = {0};
        for(int i = 0; i < str.size(); i++)//统计每个字符出现的频数
        {
            count[str[i] - 'a']++;
        }
        bool flag = false;//用户判断是否存在只出现一次的字符
        for(int i = 0; i < str.size(); i++)
        {
            if (count[str[i] - 'a'] == 1)//判断当前字符是否只出现一次
            {
                cout<<str[i]<<endl;
                flag = true;//改变flag
                break;
            }
        }
        if(!flag){//若flag为false表示不存在只出现一次的字符
            cout<<-1<<endl;
        }
    }
    return 0;
}
点击并拖拽以移动

HJ60 查找组成一个偶数最接近的两个素数

描述

任意一个偶数（大于2）都可以由2个素数组成，组成偶数的2个素数有很多种情况，本题目要求输出组成指定偶数的两个素数差值最小的素数对。

数据范围：输入的数据满足 4≤n≤1000

输入描述：

输入一个大于2的偶数

输出描述：

从小到大输出两个素数

方法一：穷举

​

点击并拖拽以移动
#include<iostream>
using namespace std;

bool isPrime(int n){ //判断数字n是否是素数
    for(int i = 2; i < n; i++){ //遍历到n-1
        if(n % i == 0) //如果由因子就不是素数
            return false;
    }
    return true; //遍历完都没有就是素数
}

int main(){
    int n;
    while(cin >> n){
        int mindis = n;
        pair<int, int> res; //记录两个素数
        for(int i = 2; i < n; i++){ //遍历2到n找到两个素数
            if(isPrime(i) && isPrime(n - i)){ //两个数都是素数的时候
                if(abs(n - i - i) < mindis){ //找距离最小
                    res = {i, n - i}; //更新最小
                    mindis = abs(n - i - i);
                }
            }
        }
        cout << res.first << endl << res.second << endl;
    } 
    return 0;
}
点击并拖拽以移动

方法二：穷举优化

​

点击并拖拽以移动
#include<iostream>
#include<math.h>
using namespace std;

bool isPrime(int n){ //判断数字n是否是素数
    for(int i = 2; i * i <= n; i++){ //遍历到根号n
        if(n % i == 0)
            return false;
    }
    return true;
}

int main(){
    int n;
    while(cin >> n){
        int mindis = n;
        pair<int, int> res; //记录两个素数
        for(int i = n / 2; i > 1; i--){ //从n的中间开始找
            if(isPrime(i) && isPrime(n - i)){ //第一次遇见两个数都是素数的时候距离从小
                cout << i << endl << n - i << endl;
                break;
            }
        }
    } 
    return 0;
}
点击并拖拽以移动

续[[华为机试61-75]]

已到达文章底部，欢迎留言、表情互动~
  • 赞一个
    0
    赞一个
  • 支持下
    0
    支持下
  • 有点酷
    0
    有点酷
  • 啥玩意
    0
    啥玩意
  • 看不懂
    0
    看不懂
0  字
评论
  • 按正序
  • 按倒序
  • 按热度
Powered by Waline v2.15.2