HJ61 放苹果

约 10303 字大约 34 分钟...

HJ61 放苹果

描述

把m个同样的苹果放在n个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的分法？

注意：如果有7个苹果和3个盘子，（5，1，1）和（1，5，1）被视为是同一种分法。

数据范围：0≤m≤10 ，1≤n≤10 。

输入描述：

输入两个int整数

输出描述：

输出结果，int型

解法一：dfs

#include <iostream>
using namespace std;

int dfs(int m, int n) {
    if (m == 0) return 1; // 第一种情况，我们的苹果的数量为 0
    if (n == 1) return 1; // 第二种情况，我们只剩下了一个盘子
    if (m < n) return dfs(m, m); // 如果我们的苹果数量小于了我们的盘子的数量，我们让盘子数量等于苹果的数量
    return (dfs(m - n, n) + dfs(m, n - 1)); // 其他情况的时候，我们要计算少一个盘子，和所有盘子拿走一个苹果的情况，最后就是答案
}
void solve() {
    int m, n;
    while(cin >> m >> n) {  // 多组输入我们的 m 和 n
        cout << dfs(m, n) << "\n"; // dfs最后返回的就是我们的答案
    }
}
signed main()
{
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    solve();
    return 0;
}

解法二：动态规划

#include <iostream>
#include <cstring>
using namespace std;

const int N = 20;
int dp[N][N], n, m;
// n个盘子，m个苹果，dp[i][j]代表i个苹果，j个盘子有多少种放的方法

void solve() {    
    while(cin >> m >> n) {
        memset(dp, 0, sizeof dp); // 清空我们的这个二维的dp数组
        for (int i = 1; i <= n; i++) dp[0][i] = 1; // 把苹果数量为1的，选法置为1
        for (int i = 1; i <= m; i++) dp[i][1] = 1; // 把盘子数置为1的，选法置为1
        for (int i = 1; i <= m; i++) { 
            for (int j = 1; j <= n; j++) {
                if (i < j) dp[i][j] = dp[i][i]; // 如果盘子数量大于苹果的数量，那么转移方程
                else dp[i][j] = dp[i - j][j] + dp[i][j - 1]; // 如果苹果数量大于等于盘子的数量，我们将他们转移为二者相加
            }
        }
        cout << dp[m][n] << "\n"; // 输出最后的答案
    }
}   
signed main()
{
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    solve();
    return 0;
}

HJ62 查找输入整数二进制中1的个数

描述

输入一个正整数，计算它在二进制下的1的个数。

注意多组输入输出！！！！！！

数据范围： 1≤n≤231−1

输入描述：

输入一个整数

输出描述：

计算整数二进制中1的个数

解法一：运用位运算进行操作

#include <iostream>
using namespace std;

int n, res; // 定义我们输入的 n 和我们最后的二进制1的个数
void solve() {
    while(cin >> n) { // 多组输入我们的 n
        res = 0; // 因为是多组输入，我们把我们每次的答案都先清空为 0
        while(n) { // 如果 n 还有数字，不为0
            if (n & 1) res++; // 如果当前 n 的最后一位二进制位是 1， 答案加1
            n >>= 1; // n 向右移一次，将刚才计算过的二进制位剔除掉
        }
        cout << res << "\n"; // 输出最后的一个答案
    }
}
signed main() {
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    solve();
    return 0;
}

解法二： STL容器

#include <iostream>
#include <bitset> // bitset在这个bitset的库里
using namespace std;

void solve() {
    int n;
    while(cin >> n) { // 多组输入一个n
        bitset<32> a = n; // 建立一个bitset，这个尖括号里面存的是位数，将n变成二进制存到a中
        cout << a.count() << "\n";  // 调用bitset的库函数输出二进制里面的1
    }
}
signed main() {
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    solve();
    return 0;
}

方法三：转化二进制字符串

#include<iostream>
#include<string>
using namespace std;

int main(){
    int n;
    while(cin >> n){
        int count = 0;
        string s = "";
        while(n){ //十进制转化成二进制
            s += ((n % 2) + '0'); //用字符串记录二进制每一位
            n /= 2;
        }
        for(int i = 0; i < s.length(); i++) //遍历字符串统计1的个数
            if(s[i] == '1')
                count++;
        cout<< count << endl;
    }
    return 0;
}

方法四：移位运算和位与运算

#include<iostream>
using namespace std;

int main(){
    int n;
    while(cin >> n){
        int count = 0;
        while(n){
            if(n & 1) //和最后一位按位与运算
                count++; //与的结果是1说明这位是1
            n >>= 1; //移位
        }
        cout<< count << endl;
    }
    return 0;
}

方法五：位与运算去掉二进制末尾1

#include<iostream>
using namespace std;

int main(){
    int n;
    while(cin >> n){
        int count = 0;
        while(n){
            count++; //统计+1
            n &= (n - 1); //去掉末尾的1
        }
        cout<< count << endl; //输出
    }
    return 0;
}

方法六：库函数

#include<iostream>
#include<bitset>
using namespace std;

int main(){
    int n;
    while(cin >> n){
        bitset<32> bit(n); //转换32位二进制类
        cout << bit.count() << endl; //直接输出位数
    }
    return 0;
}

HJ63 DNA序列

描述

一个 DNA 序列由 A/C/G/T 四个字母的排列组合组成。 G 和 C 的比例（定义为 GC-Ratio ）是序列中 G 和 C 两个字母的总的出现次数除以总的字母数目（也就是序列长度）。在基因工程中，这个比例非常重要。因为高的 GC-Ratio 可能是基因的起始点。

给定一个很长的 DNA 序列，以及限定的子串长度 N ，请帮助研究人员在给出的 DNA 序列中从左往右找出 GC-Ratio 最高且长度为 N 的第一个子串。

DNA序列为 ACGT 的子串有: ACG , CG , CGT 等等，但是没有 AGT ， CT 等等

数据范围：字符串长度满足 1≤n≤1000 ，输入的字符串只包含 A/C/G/T 字母

输入描述：

输入一个string型基因序列，和int型子串的长度

输出描述：

找出GC比例最高的子串,如果有多个则输出第一个的子串

方法一：暴力解法

#include<iostream>
#include<string>
using namespace std;

int main(){
    string s;
    int n;
    while(cin >> s >> n){
        int len = s.length();
        int resindex = 0, max = 0;
        for(int i = 0; i + n < len; i++){ //遍历字符串每一位，从该位开始
            int count = 0;
            for(int j = 0; j < n; j++){ //从i位起长为n的字符串
                if(s[i + j] == 'G' || s[i + j] == 'C') //统计CG出现次数
                    count++; 
            }
            if(count > max){ //取次数更多的
                resindex = i; //得到序列起始下标
                max = count;
            }
        }
        cout << s.substr(resindex, n) << endl; //根据下标和n输出
    }
    return 0;
}

方法二：滑动窗口

#include<iostream>
#include<string>
using namespace std;

int main(){
    string s;
    int n;
    while(cin >> s >> n){
        int len = s.length();
        int resindex = 0, max = 0;
        int count = 0;
        for(int i = 0; i < n; i++) //录入最前面的窗口
            if(s[i] == 'C' || s[i] == 'G')
                count++;
        max = count; //录下第一个窗口的CG数量作为最大
        int left = 1, right = n; //从录入窗口的左右点右移一位开始
        while(right < len){ //直到右窗口结束
            if(s[left - 1] == 'C' || s[left - 1] == 'G') //窗口左边出去的是CG
                count--;
            if(s[right] == 'C' || s[right] == 'G') //窗口右边进来的是CG
                count++;
            if(count > max){ //更新，取最大值
                max = count;
                resindex = left;
            }
            left++;
            right++;
        }
        cout << s.substr(resindex, n) << endl; //根据下标和n输出
    }
    return 0;
}

HJ64 MP3光标位置

描述

MP3 Player因为屏幕较小，显示歌曲列表的时候每屏只能显示几首歌曲，用户要通过上下键才能浏览所有的歌曲。为了简化处理，假设每屏只能显示4首歌曲，光标初始的位置为第1首歌。

现在要实现通过上下键控制光标移动来浏览歌曲列表，控制逻辑如下：

歌曲总数<=4的时候，不需要翻页，只是挪动光标位置。

光标在第一首歌曲上时，按Up键光标挪到最后一首歌曲；光标在最后一首歌曲时，按Down键光标挪到第一首歌曲。

其他情况下用户按Up键，光标挪到上一首歌曲；用户按Down键，光标挪到下一首歌曲。

2. 歌曲总数大于4的时候（以一共有10首歌为例）：

特殊翻页：屏幕显示的是第一页（即显示第1 – 4首）时，光标在第一首歌曲上，用户按Up键后，屏幕要显示最后一页（即显示第7-10首歌），同时光标放到最后一首歌上。同样的，屏幕显示最后一页时，光标在最后一首歌曲上，用户按Down键，屏幕要显示第一页，光标挪到第一首歌上。

一般翻页：屏幕显示的不是第一页时，光标在当前屏幕显示的第一首歌曲时，用户按Up键后，屏幕从当前歌曲的上一首开始显示，光标也挪到上一首歌曲。光标当前屏幕的最后一首歌时的Down键处理也类似。

其他情况，不用翻页，只是挪动光标就行。

数据范围：命令长度1≤s≤100 ，歌曲数量1≤n≤150

进阶：时间复杂度：O(n) ，空间复杂度：O(n)

输入描述：

输入说明：
1 输入歌曲数量
2 输入命令 U或者D

输出描述：

输出说明
1 输出当前列表
2 输出当前选中歌曲

方法一：模拟

#include <iostream>
#include <string>
using namespace std;

int main(){
    int n;
    string commands;
    while(cin >> n >> commands){
        int num = 1;
        // first：当前屏幕显示页的第一首歌曲的编号
        int first = 1;
        // 歌曲总数不超过4时，不需翻页
        if(n <= 4) {
            for(int i = 0; i < commands.size(); i++){
                // 特殊向上翻页
                if(num == 1 && commands[i] == 'U'){
                    num = n; 
                // 特殊向下翻页
                }else if(num == n && commands[i] == 'D'){
                    num = 1;
                }else if(commands[i] == 'U'){
                    num--;
                }else{
                    num++; 
                }
            }
            for(int i = 1; i <= n - 1; i++){//输出当前页
                cout << i << ' ';
            }
            cout << n << endl << num << endl;
        }else{// 歌曲总数大于4时，需要翻页
            for(int i = 0; i < commands.size(); i++){
                // 特殊向上翻页
                if(num == 1 && commands[i] == 'U') {
                    first = n-3;
                    num = n;
                }else if(num == n && commands[i] == 'D') {// 特殊向下翻页
                    first = 1;
                    num = 1;
                }else if(num == first && commands[i] == 'U')//一般向上翻页
                {
                    first--;
                    num--;
                }else if(num == first + 3 && commands[i] == 'D')//一般向下翻页
                {
                    first++;
                    num++;
                }else if(commands[i] == 'U'){//其他情况，不翻页，只移动光标
                    num--;
                }else{
                    num++;
                }
            }
            for(int i = first; i < first + 3; i++){//输出当前页面
                cout << i << ' ';
            }
            cout << first + 3 << endl << num << endl;
        }
    }
    return 0;
}

方法二：滑动窗口

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

int main(){
    int n;
    string commands;
    while(cin >> n >> commands){
        int num = 1;//选中的歌曲
        int win_b = 1;//页面的起始
        int win_e = min(4,n);//页面的末位置
        for(int i = 0; i < commands.size(); i++){
            if(commands[i] == 'U') {//向上移动一格
                num = (num-1-1+n)%n + 1;
            }else if(commands[i] == 'D') {//向下移动一格
                num = num % n + 1;
            }
            if(num < win_b){//如果当前歌曲在窗口前，则将窗口往前移动
                win_b = num;
                win_e = win_b + 3;
            }else if(num > win_e){//如果当前歌曲在窗口后，则将窗口往后移动
                win_e = num;
                win_b = win_e - 3;
            }
        }
        for(int i = win_b; i <= win_e; i++){//输出当前页面
            cout << i << ' ';
        }
        cout << endl;
        cout << num << endl;//输出选中的歌曲
    }
    return 0;
}

HJ65 查找两个字符串a,b中的最长公共子串

描述

查找两个字符串a,b中的最长公共子串。若有多个，输出在较短串中最先出现的那个。

注：子串的定义：将一个字符串删去前缀和后缀（也可以不删）形成的字符串。请和“子序列”的概念分开！

数据范围：字符串长度1≤length≤300

进阶：时间复杂度：O(n^3) ，空间复杂度：O(n)

输入描述：

输入两个字符串

输出描述：

返回重复出现的字符

方法一：暴力枚举

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;

int main(){
    string s1, s2;
    while(cin >> s1 >> s2){
        if(s1.length() > s2.length()) //使较小的字符串在前
            swap(s1, s2);
        string output = "";
        for(int i = 0; i < s1.length(); i++){ //遍历s1每个起始点的每个长度
            for(int j = i; j < s1.length(); j++){
                if(int(s2.find(s1.substr(i, j - i + 1))) < 0) //截取子串能够在s2中被找到
                    break;
                else if(output.length() < j - i + 1) //更新较长的子串
                    output = s1.substr(i, j - i + 1);
            }
        }
        cout << output << endl;
    }
    return 0;
}

方法二：枚举改进

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;

int main(){
    string s1, s2;
    while(cin >> s1 >> s2){
        if(s1.length() > s2.length()) //使较小的字符串在前
            swap(s1, s2);
        string output = "";
        for(int i = 0; i < s1.length(); i++){ //遍历s1每个起始点
            for(int j = 0; j < s2.length(); j++){ //遍历s2每个起点
                int length = 0;
                int x = i, y = j;
                while(x < s1.length() && y < s2.length() && s1[x] == s2[y]){ //比较每个起点为始的子串
                    x++;
                    y++;
                    length++;
                }
                if(output.length() < length) //更新更大的长度子串
                    output = s1.substr(i, x - i);
            }
        }
        cout << output << endl;
    }
    return 0;
}

方法三：动态规划

#include<iostream>
#include<string>
#include<vector>
using namespace std;

int main(){
    string s1, s2;
    while(cin >> s1 >> s2){
        if(s1.length() > s2.length()) //使较小的字符串在前
            swap(s1, s2);
        vector<vector<int> > dp(s1.length() + 1, vector<int>(s2.length() + 1, 0)); //dp[i][j]表示到s1第i个个到s2第j个为止的公共子串长度
        int max = 0, end = 0;
        for(int i = 1; i <= s1.length(); i++){
            for(int j = 1; j <= s2.length(); j++){
                if(s1[i - 1] == s2[j - 1]) //如果该两位相同
                    dp[i][j] = dp[i - 1][j - 1] + 1; //则增加长度
                else //否则
                    dp[i][j] = 0; //该位置为0
                if(dp[i][j] > max){ //更新最大长度
                    max = dp[i][j];
                    end = i - 1;
                }
            }
        }
        cout << s1.substr(end - max + 1, max) << endl; //输出最长子串
    }
    return 0;
}

HJ66 配置文件恢复

描述

有6条配置命令，它们执行的结果分别是：

命令

执行

reset

reset what

reset board

board fault

board add

where to add

board delete

no board at all

reboot backplane

impossible

backplane abort

install first

he he

unknown command

注意：he he不是命令。

为了简化输入，方便用户，以“最短唯一匹配原则”匹配（注：需从首字母开始进行匹配）：

1、若只输入一字串，则只匹配一个关键字的命令行。例如输入：r，根据该规则，匹配命令reset，执行结果为：reset what；输入：res，根据该规则，匹配命令reset，执行结果为：reset what；
2、若只输入一字串，但匹配命令有两个关键字，则匹配失败。例如输入：reb，可以找到命令reboot backpalne，但是该命令有两个关键词，所有匹配失败，执行结果为：unknown command

3、若输入两字串，则先匹配第一关键字，如果有匹配，继续匹配第二关键字，如果仍不唯一，匹配失败。

例如输入：r b，找到匹配命令reset board 和 reboot backplane，执行结果为：unknown command。

例如输入：b a，无法确定是命令board add还是backplane abort，匹配失败。

4、若输入两字串，则先匹配第一关键字，如果有匹配，继续匹配第二关键字，如果唯一，匹配成功。例如输入：bo a，确定是命令board add，匹配成功。
5、若输入两字串，第一关键字匹配成功，则匹配第二关键字，若无匹配，失败。例如输入：b addr，无法匹配到相应的命令，所以执行结果为：unknow command。
6、若匹配失败，打印“unknown command”

注意：有多组输入。

数据范围：数据组数：1≤t≤800 ，字符串长度1≤s≤20

进阶：时间复杂度：O(n) ，空间复杂度：O(n)\O(n)

输入描述：

多行字符串，每行字符串一条命令

输出描述：

执行结果，每条命令输出一行

方法一：模拟存储

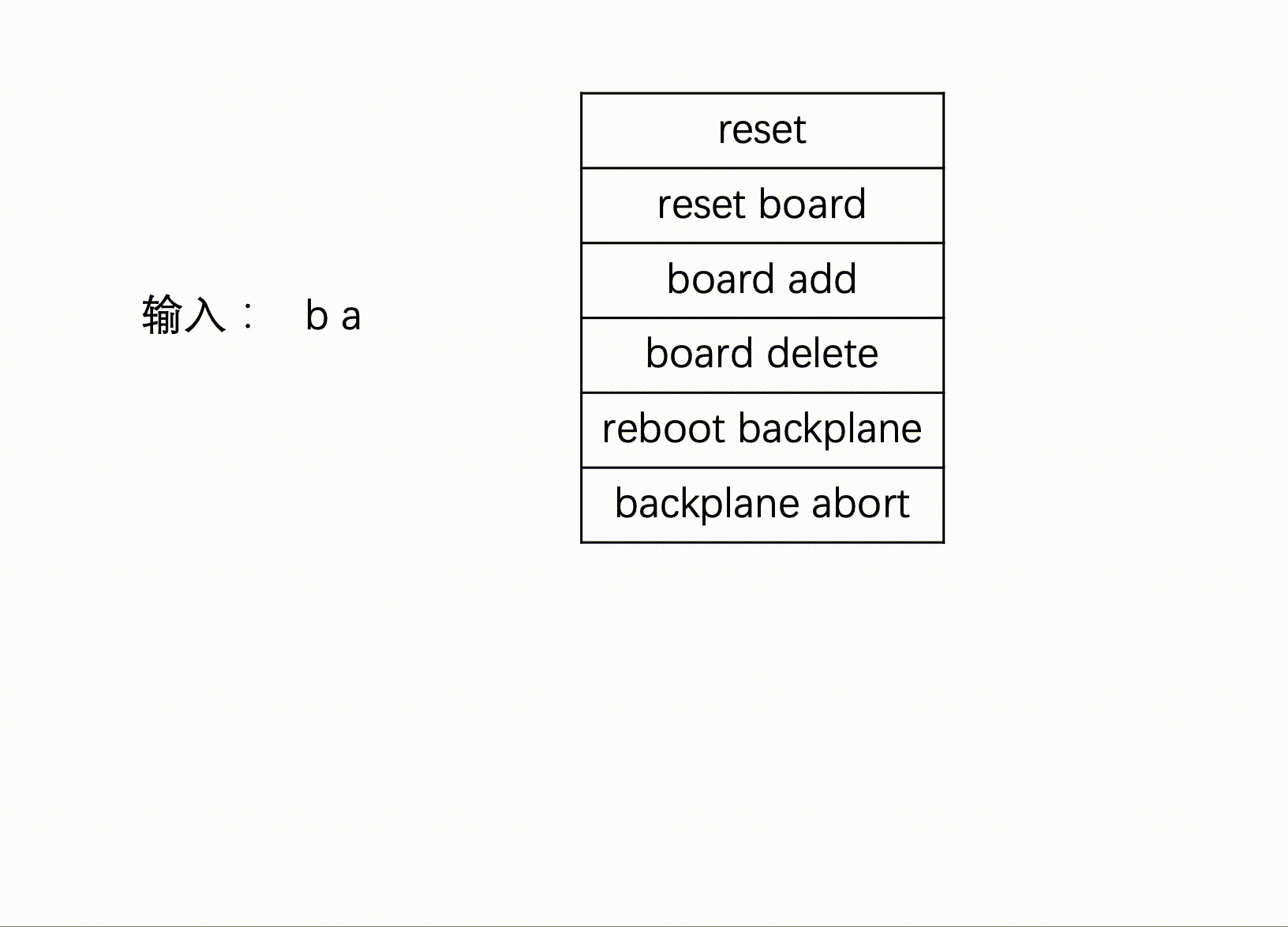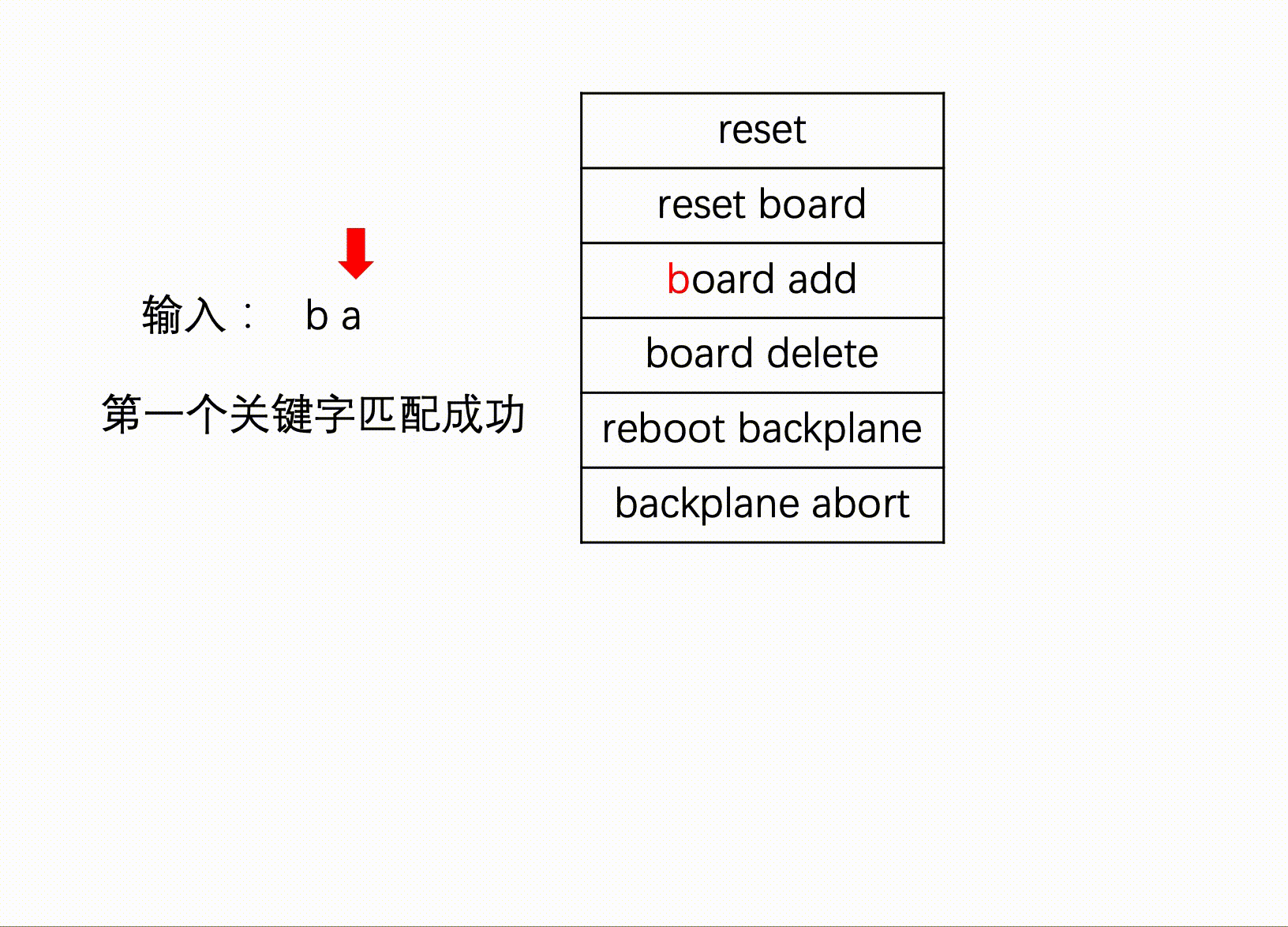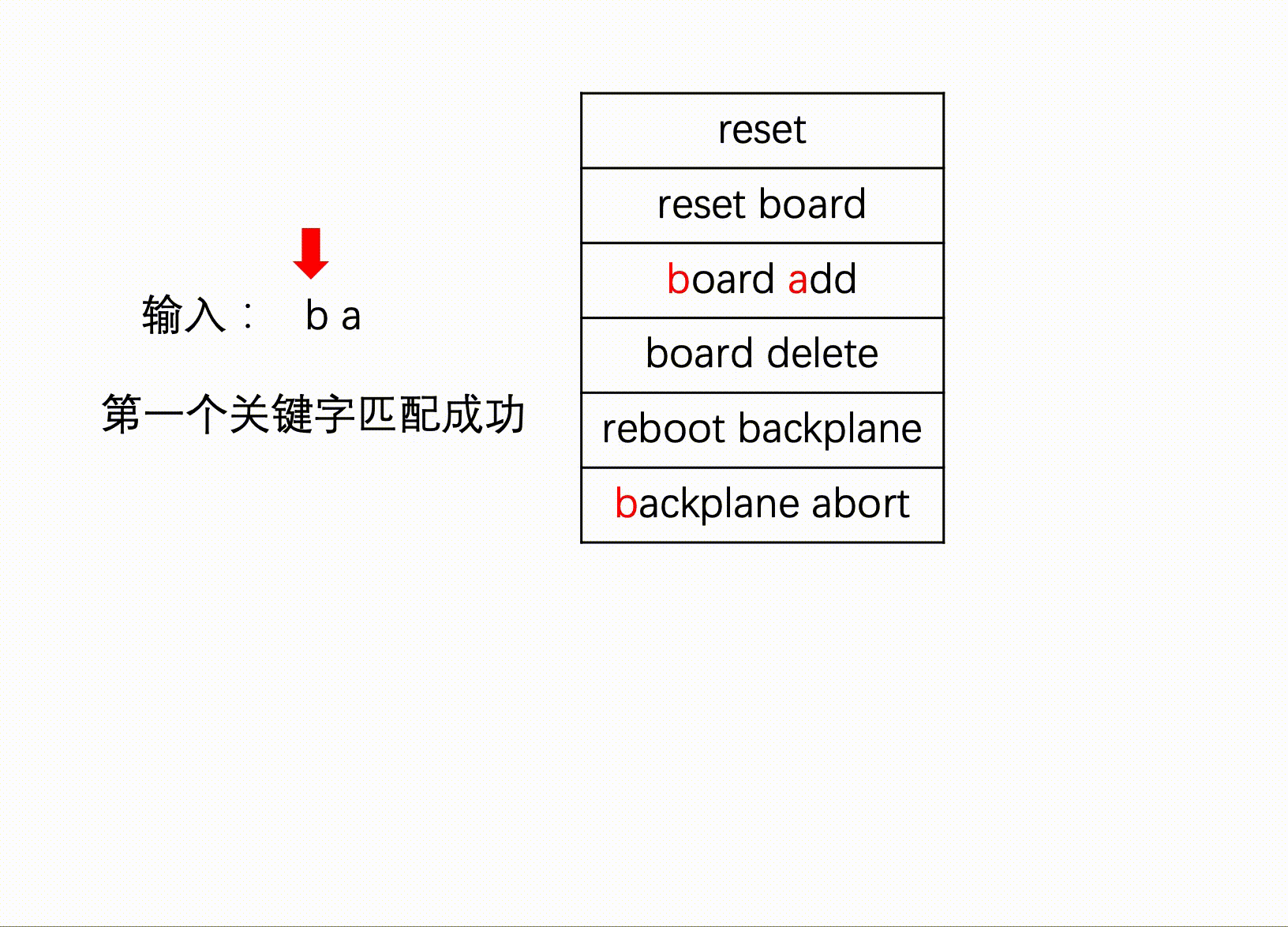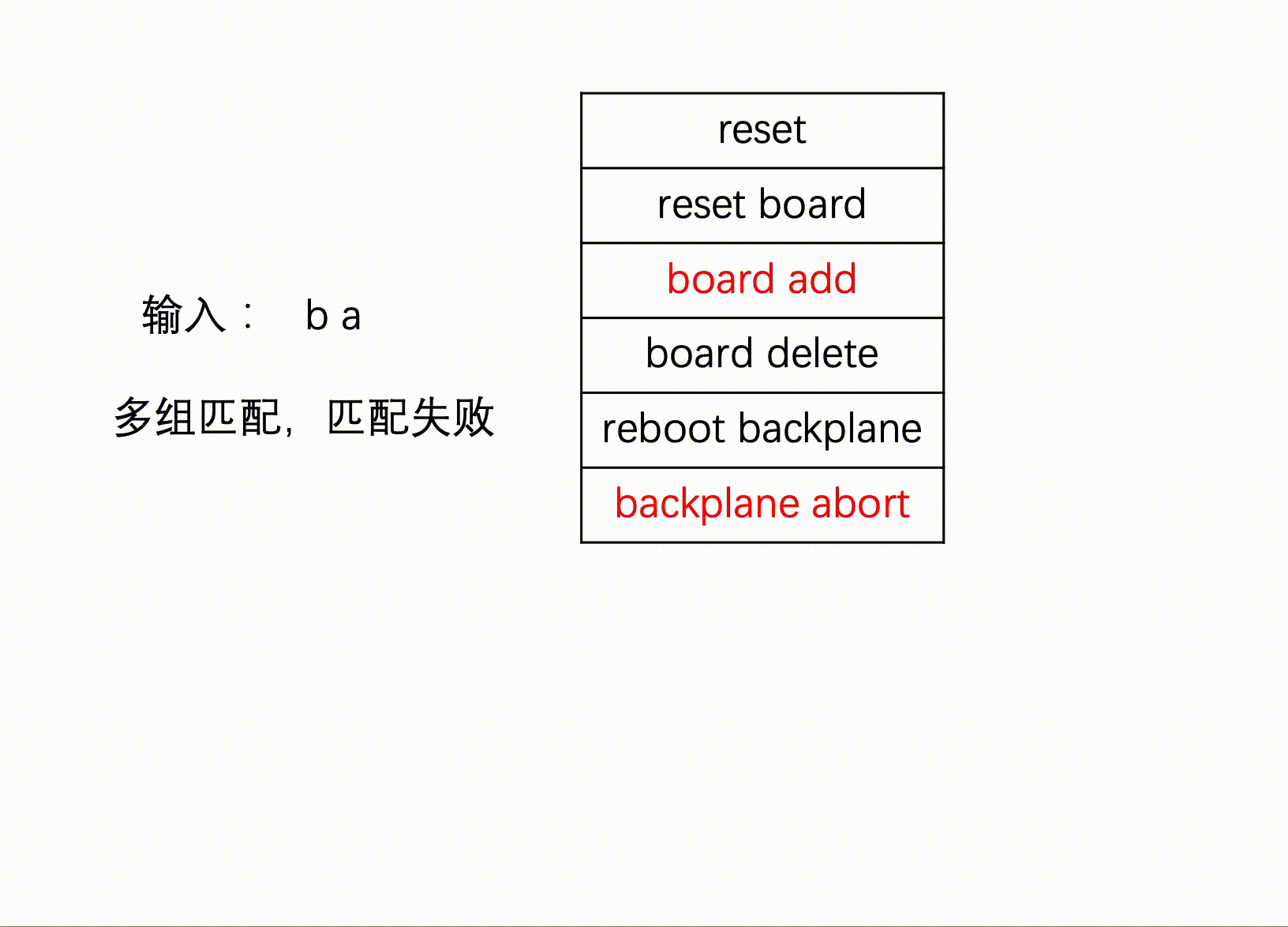
#include <iostream>
#include <string>
#include <vector>

using namespace std;

int main(){
    vector<pair<string, string>> cmdin = { { "reset","" } ,{ "reset","board" } ,{ "board","add" } ,{ "board","delete" } ,{ "reboot","backplane" } ,{ "backplane","abort" } };
    vector<string> cmdout = { "reset what" ,"board fault" ,"where to add" ,"no board at all" ,"impossible" ,"install first" };
    string s;
    while (getline(cin,s)){
        string s1 , s2;
        int pos = 0;
        //以空格为分界划分
        while (pos < s.size() && s[pos] != ' '){//遍历一遍找到空格的位置
            pos++;
        }
        s1 = s.substr(0, pos);
        if (pos != s.size()){
            s2 = s.substr(pos + 1, s.size());
        }
		int count1 = 0, count2 = 0;
		string result;
		for (auto iter=cmdin.begin();iter!=cmdin.end();iter++){
			int flag1 = iter->first.find(s1) == 0? 1 : 0;//判断第一个关键字是否匹配
			int flag2;
			if (s2 != "") {
				flag2 = iter->second.find(s2) == 0? 1 : 0;//判断第二个关键字是否匹配
			}else if(s2==""&&iter->second==""){//如果没有第二个关键字，默认匹配成功
				flag2 = 1;
			}else{
                flag2 = 0;
            }
			if (flag1 && flag2)//两个关键字都匹配上了
			{
				count1++;
				count2++;
				result = cmdout[iter - cmdin.begin()];
			}
		}
		if (count1 == 1 && count2 == 1){//两个关键字都匹配成功，且只有一组匹配
			cout << result << endl;
		}else {//匹配失败或有多组匹配
			cout << "unknown command" << endl;
		}
	}
	return 0;
}

方法二：正则表达式

#include <iostream>
#include <string>
#include <regex>
#include <vector>

using namespace std;

int main(){
    vector<pair<string, string>> cmdin = { { "reset","" } ,{ "reset","board" } ,{ "board","add" } ,{ "board","delete" } ,{ "reboot","backplane" } ,{ "backplane","abort" } };
    vector<string> cmdout = { "reset what" ,"board fault" ,"where to add" ,"no board at all" ,"impossible" ,"install first" };
    string s;
    while (getline(cin,s)){
        string s1 , s2;
        int pos = 0;
        //以空格为分界划分
        while (pos < s.size() && s[pos] != ' '){//遍历一遍找到空格的位置
            pos++;
        }
        s1 = s.substr(0, pos);
        if (pos != s.size()){
            s2 = s.substr(pos + 1, s.size());
        }
		int count1 = 0, count2 = 0;
		string result;
		for (auto iter=cmdin.begin();iter!=cmdin.end();iter++){
            string pattern1 = s1 + "[a-z]*";//正则表达式
            int flag1 = regex_match(iter->first, regex(pattern1));//第一个关键字匹配
            string pattern2 = s2 + "[a-z]*";//正则表达式
            int flag2 = 0;
            if((s2 == "" && iter->second == "")){
                flag2 = 1;
            }else if(s2 != ""){
                flag2 = regex_match(iter->second, regex(pattern2));//第二个关键字匹配
            }
            if (flag1 && flag2)//两个关键字都匹配上了
			{
				count1++;
				count2++;
				result = cmdout[iter - cmdin.begin()];
			}
		}
		if (count1 == 1 && count2 == 1){//两个关键字都匹配成功，且只有一组匹配
			cout << result << endl;
		}else {//匹配失败或有多组匹配
			cout << "unknown command" << endl;
		}
	}
	return 0;
}

HJ67 24点游戏算法

描述

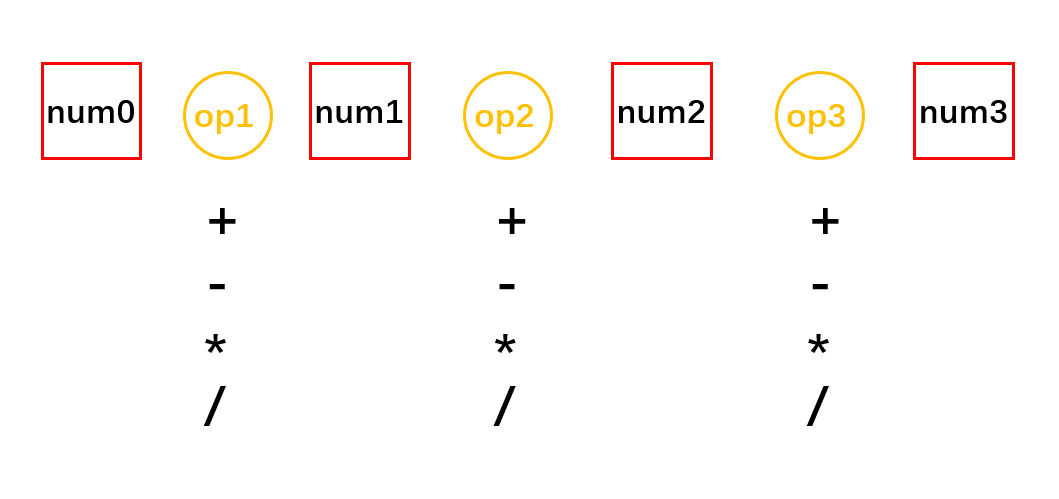
给出4个1-10的数字，通过加减乘除运算，得到数字为24就算胜利,除法指实数除法运算,运算符仅允许出现在两个数字之间,本题对数字选取顺序无要求，但每个数字仅允许使用一次，且需考虑括号运算

此题允许数字重复，如3 3 4 4为合法输入，此输入一共有两个3，但是每个数字只允许使用一次，则运算过程中两个3都被选取并进行对应的计算操作。

输入描述：

读入4个[1,10]的整数，数字允许重复，测试用例保证无异常数字。

输出描述：

对于每组案例，输出一行表示能否得到24点，能输出true，不能输出false

方法一：穷举遍历

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

double cal(double a, double b, char c){ //根据运算符运算结果
    switch(c){
        case '+': return a + b;
        case '-': return a - b;
        case '*': return a * b;
        case '/': return a / b;
    }
    return 0;
}

bool check(vector<double>& nums){
    char op[4] = {'+', '-', '*', '/'};
    sort(nums.begin(), nums.end()); //先按照从小到大排
    do{
          for(int i = 0; i < 4; i++) //遍历三个位置的所有可能运算符
              for(int j = 0; j < 4; j++)
                  for(int k = 0; k < 4; k++){
                      double first = cal(nums[0], nums[1], op[i]); //依次运算
                      double second = cal(first, nums[2], op[j]);
                      if(cal(second, nums[3], op[k]) == 24) //判断是否等于24
                          return true;
                  }
      }while(next_permutation(nums.begin(), nums.end())); //依次找到其他排列
    return false;
}

int main(){
    vector<double> nums(4); 
    while(cin >> nums[0] >> nums[1] >> nums[2] >> nums[3]){ //输入4个数字
        if(check(nums))
            cout << "true" << endl;
        else
            cout << "false" << endl;
    }
    return 0;
}

方法二：递归搜索

#include<iostream>
#include<vector>
using namespace std;

bool check(vector<double> nums, double result){ //递归检查能否组成24
    if(nums.empty()) //数组为空，判断等不等于24
        return result == 24;
    for(int i = 0; i < nums.size(); i++){ //遍历剩下的数字
        vector<double> rest(nums);
        rest.erase(rest.begin() + i); //删去使用的数字
        if(check(rest, result + nums[i]) //分别 进行加减乘除4种运算
          || check(rest, result - nums[i])
          || check(rest, result * nums[i])
          || check(rest, result / nums[i]))
            return true;
    }
    return false;
}

int main(){
    vector<double> nums(4); 
    while(cin >> nums[0] >> nums[1] >> nums[2] >> nums[3]){ //输入4个数字
        if(check(nums, 0))
            cout << "true" << endl;
        else
            cout << "false" << endl;
    }
    return 0;
}

HJ68 成绩排序

描述

给定一些同学的信息（名字，成绩）序列，请你将他们的信息按照成绩从高到低或从低到高的排列,相同成绩

都按先录入排列在前的规则处理。

例示：
jack      70
peter     96
Tom       70
smith     67

从高到低  成绩
peter     96
jack      70
Tom       70
smith     67

从低到高

smith 67

jack 70

Tom 70

peter 96

注：0代表从高到低，1代表从低到高

数据范围：人数：1≤n≤200

进阶：时间复杂度：O(nlogn) ，空间复杂度：O(n)

输入描述：

第一行输入要排序的人的个数n，第二行输入一个整数表示排序的方式，之后n行分别输入他们的名字和成绩，以一个空格隔开

输出描述：

按照指定方式输出名字和成绩，名字和成绩之间以一个空格隔开

方法一：库函数

#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
using namespace std;

bool cmp0(const pair<string, int>& a, const pair<string, int>& b) { //重载降序比较
    return a.second > b.second;
}
 
bool cmp1(const pair<string, int>& a, const pair<string, int>& b) { //重载升序比较
    return a.second < b.second;
}
int main()
{
    int n, flag;
    while (cin >> n >> flag) { 
        vector<pair<string, int>> record(n); //记录名字和成绩
        for (int i = 0; i < n; i++) { //输入成绩
            string name;
            int grade;
            cin >> name;
            cin>> grade;
            record[i].first = name;
            record[i].second = grade;
        }
        if (flag == 0) { //根据flag决定升序还是降序
            stable_sort(record.begin(), record.end(), cmp0);
        }
        else {
            stable_sort(record.begin(), record.end(), cmp1);
        }      
        for (int i = 0; i < n; i++) { //输出
            cout << record[i].first << ' ' << record[i].second << endl;
        }
    }
    return 0;
}

方法二：桶排序

#include<iostream>
#include<string>
#include<vector>
using namespace std;

int main()
{
    int n, flag;
    while (cin >> n >> flag) { 
        vector<string> score[101]; // 准备0-100分的桶
        for(int i = 0; i < n; i++){ //输入n个数据
            string name;
            int grade;
            cin >> name >> grade;
            score[grade].push_back(name); //将相应分数后面加入名字
        }
        if(flag == 0){ //降序
            for(int i = 100; i >= 0; i--){ //从100开始依次输出每个名字和分数
                for(int j = 0; j < score[i].size(); j++)
                    cout << score[i][j] << " " << i << endl;
            }
        }else{ //升序
            for(int i = 0; i <= 100; i++){ //从0开始依次输出每个名字和分数
                for(int j = 0; j < score[i].size(); j++)
                    cout << score[i][j] << " " << i << endl;
            }
        }
    }
    return 0;
}

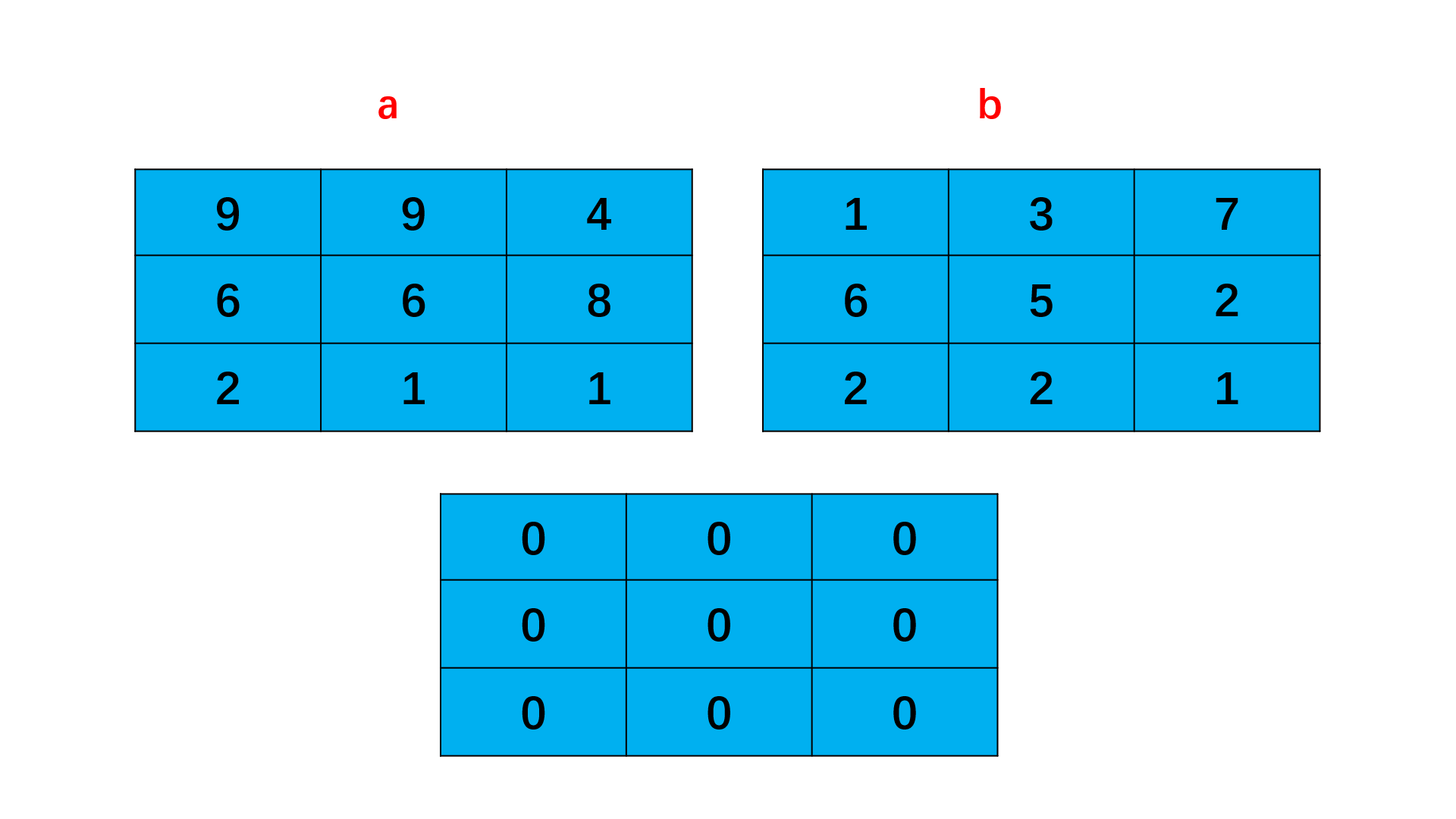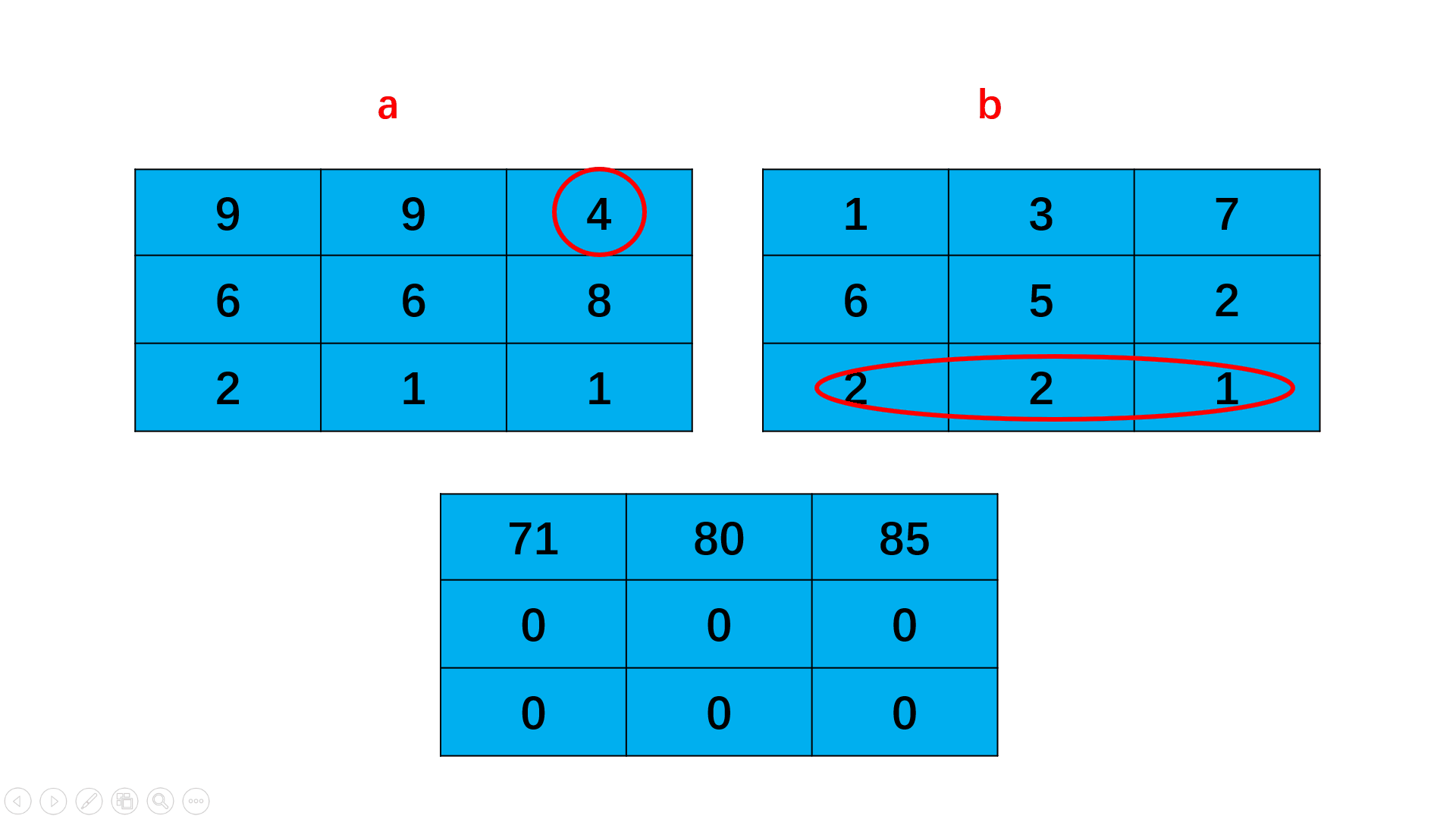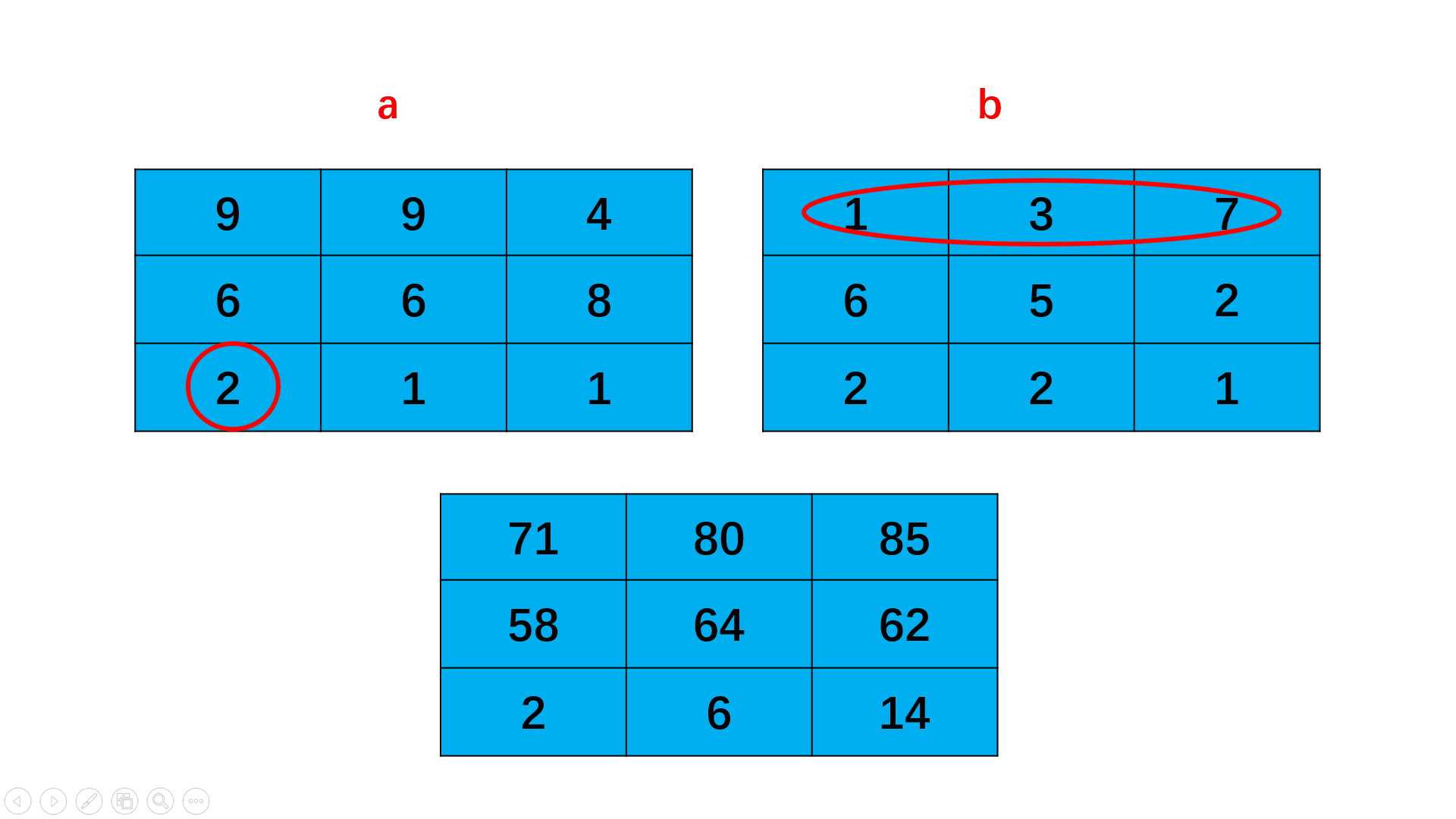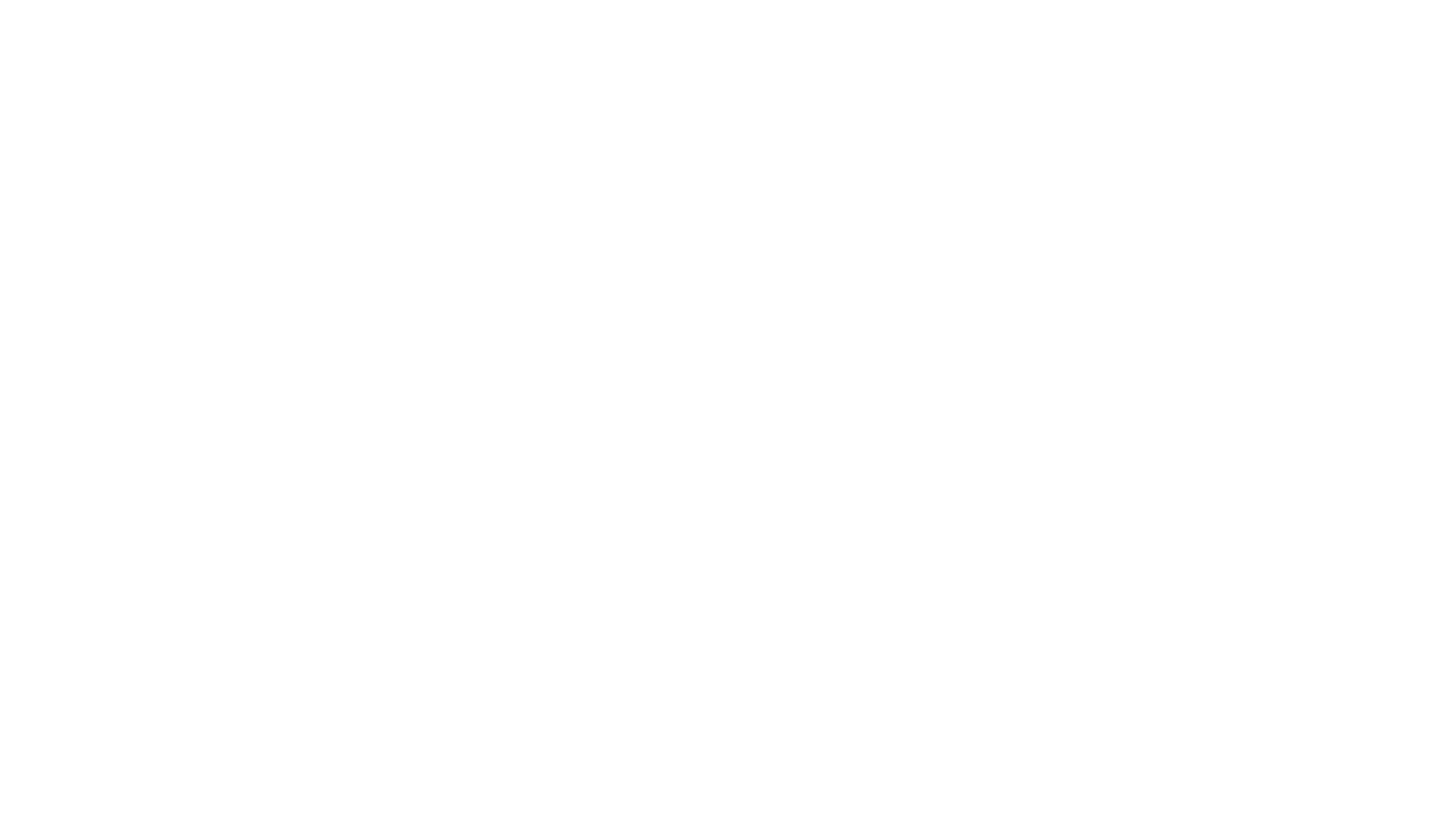
HJ69 矩阵乘法

输入描述：

第一行包含一个正整数x，代表第一个矩阵的行数
第二行包含一个正整数y，代表第一个矩阵的列数和第二个矩阵的行数
第三行包含一个正整数z，代表第二个矩阵的列数
之后x行，每行y个整数，代表第一个矩阵的值
之后y行，每行z个整数，代表第二个矩阵的值

输出描述：

对于每组输入数据，输出x行，每行z个整数，代表两个矩阵相乘的结果

方法一：

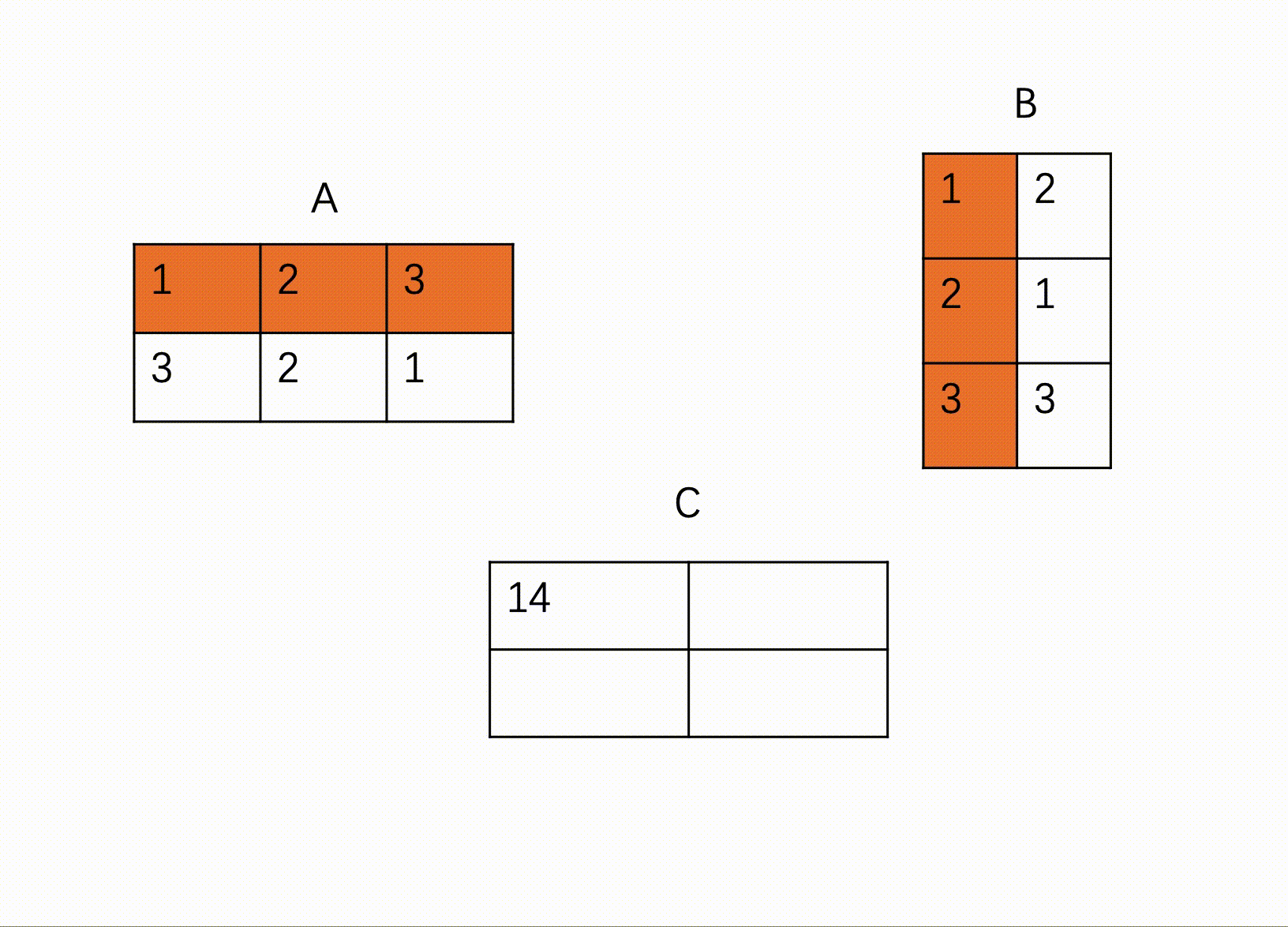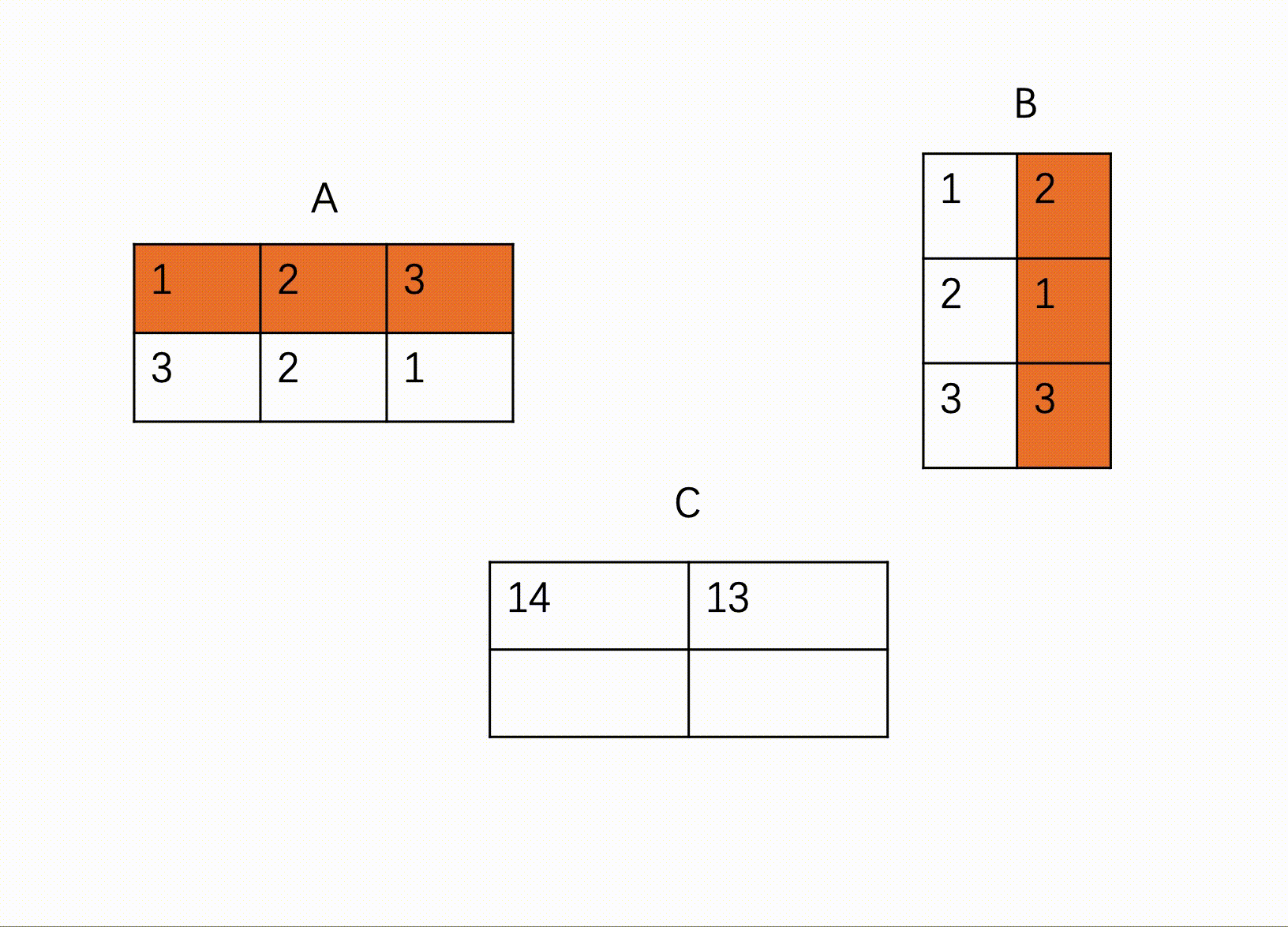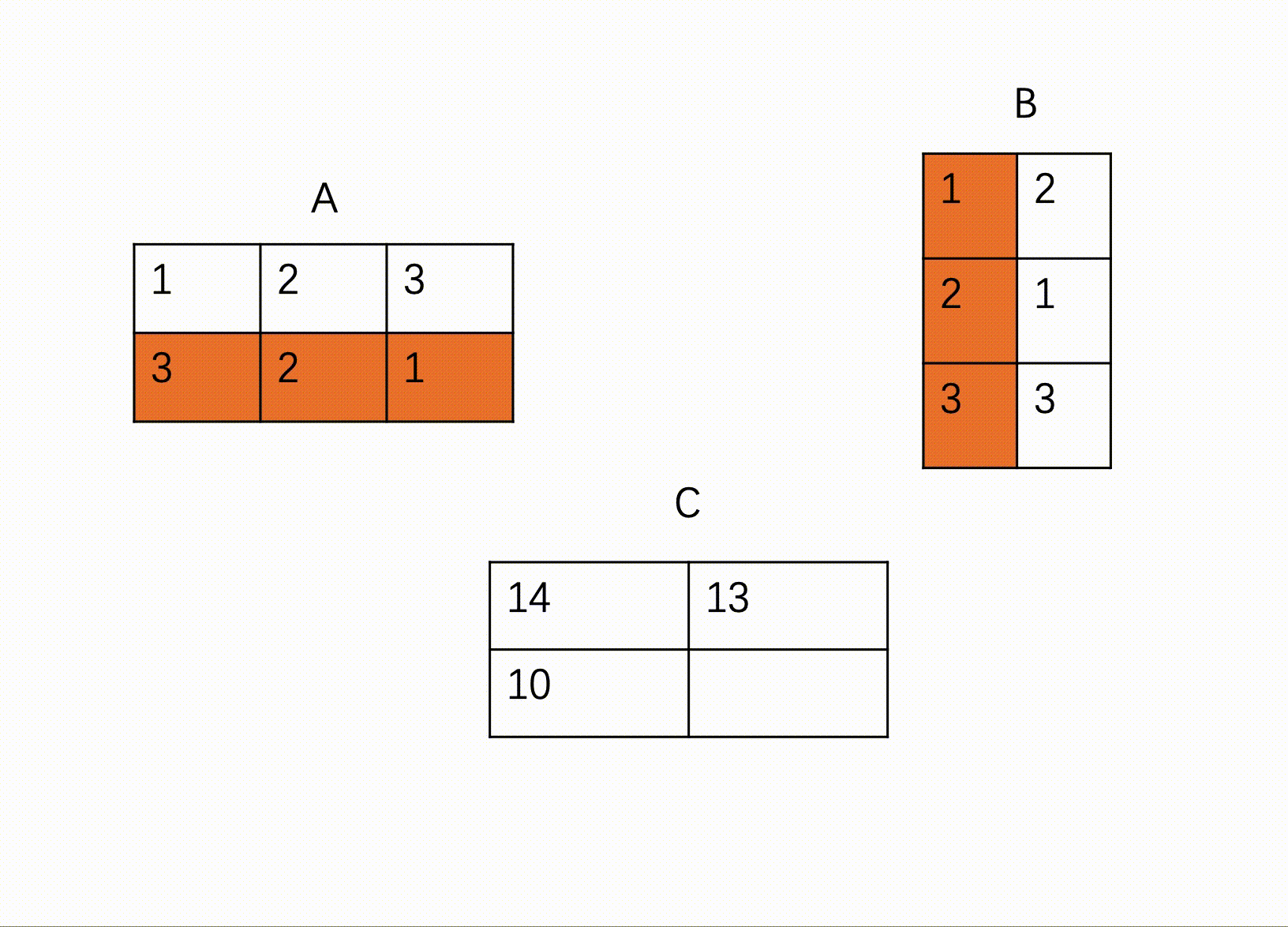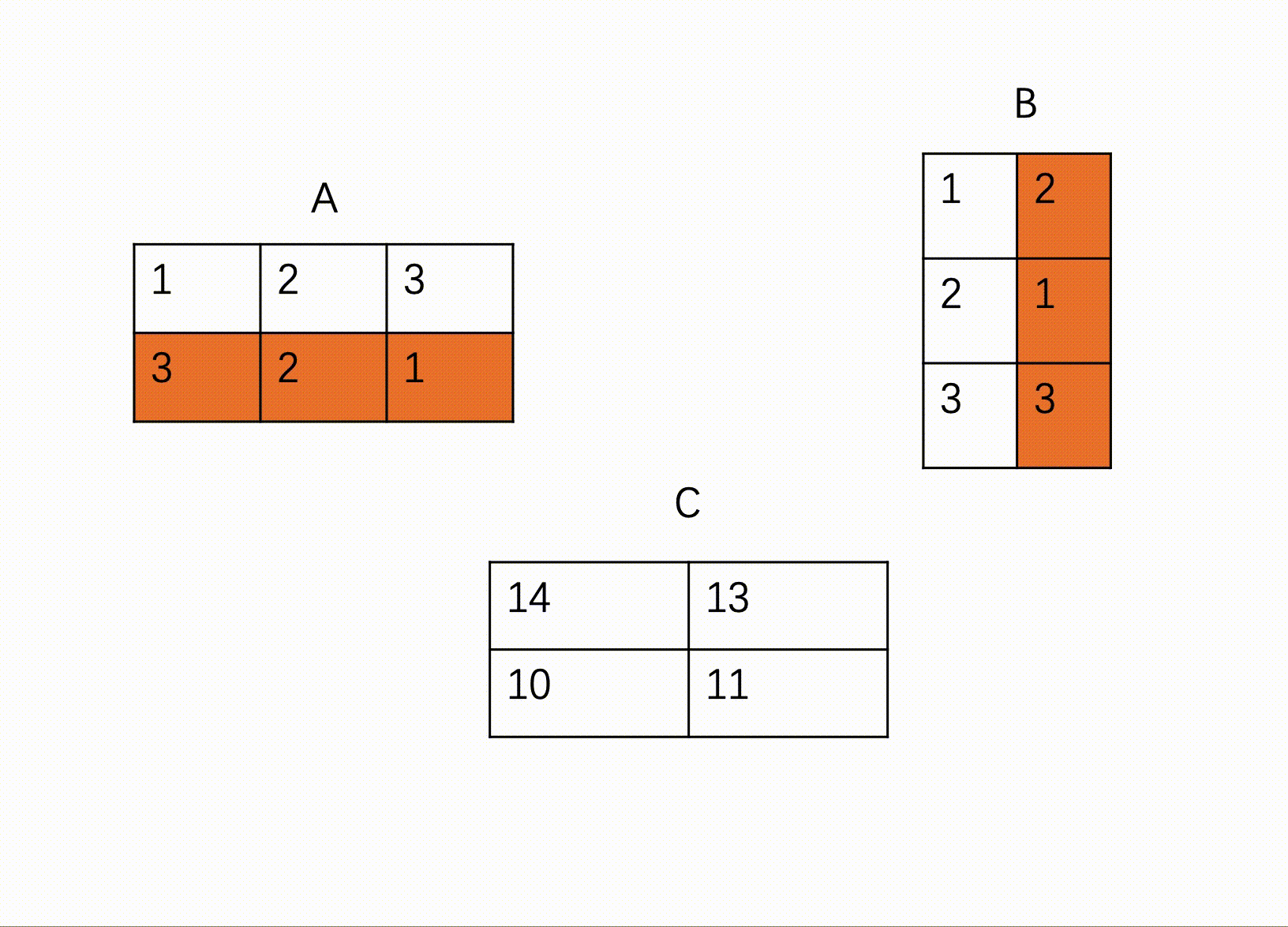
#include<iostream>
#include<vector>
using namespace std;
int main(){
    int x, y, z;
    while (cin >> x >> y >> z){
        vector<vector<int>> A(x, vector<int>(y, 0));
        vector<vector<int>> B(y, vector<int>(z, 0));
        vector<vector<int>> C(x, vector<int>(z, 0));
        for(int i = 0; i < x; ++i){//输入矩阵A
            for(int j = 0; j < y; ++j)
                cin >> A[i][j];
        }
        for(int i = 0; i < y; ++i){//输入矩阵B
            for(int j = 0; j < z; ++j)
                cin >> B[i][j];
        }
        for(int i = 0; i < x; ++i){//计算C[i][j]的值
            for(int j = 0; j < z; ++j)
                for(int k = 0; k < y; ++k)//A的第i行和B的第j列相乘的结果为C[i][j]
                    C[i][j] += A[i][k] * B[k][j];
        }
        for(int i = 0; i < x; ++i){//输出C
            for(int j = 0; j < z-1; ++j)
                cout << C[i][j] << " ";
            cout << C[i][z-1] << endl;
        }
    }
    return 0;
}

方法二：

#include<iostream>
#include<vector>
using namespace std;
int main(){
    int x, y, z;
    while (cin >> x >> y >> z){
        vector<vector<int>> A(x, vector<int>(y, 0));
        vector<vector<int>> B(y, vector<int>(z, 0));
        vector<vector<int>> C(x, vector<int>(z, 0));
        for(int i = 0; i < x; ++i){//输入矩阵A
            for(int j = 0; j < y; ++j)
                cin >> A[i][j];
        }
        for(int i = 0; i < y; ++i){//输入矩阵B
            for(int j = 0; j < z; ++j)
                cin >> B[i][j];
        }
        for(int i = 0; i < x; ++i){
            for(int j = 0; j < y; ++j){
                for(int k = 0; k < z; ++k){//计算C第i行的值
                    C[i][k] += A[i][j] * B[j][k];
                }
            }
        }
        for(int i = 0; i < x; ++i){//输出C
            for(int j = 0; j < z-1; ++j)
                cout << C[i][j] << " ";
            cout << C[i][z-1] << endl;
        }
    }
    return 0;
}

方法三：暴力法

#include<iostream>
#include<vector>
using namespace std;

int main(){
    int x, y, z;
    while(cin >> x >> y >> z){
        vector<vector<int> > A(x, vector<int>(y, 0));
        vector<vector<int> > B(y, vector<int>(z, 0));
        for(int i = 0; i < x; i++) //输入两个矩阵
            for(int j = 0; j < y; j++)
                cin >> A[i][j];
        for(int i = 0; i < y; i++)
            for(int j = 0; j < z; j++)
                cin >> B[i][j];
        vector<vector<int> > C(x, vector<int>(z, 0)); //构建结果矩阵
        for(int i = 0; i < x; i++) //遍历相乘相加
            for(int j = 0; j < y; j++)
                for(int k = 0; k < z; k++)
                    C[i][k] += A[i][j] * B[j][k]; //行*列相加
        for(int i = 0; i < x; i++){ //输出
            for(int j = 0; j < z; j++)
                cout << C[i][j] << " ";
            cout << endl;
        }
    }
    return 0;
}

方法四：暴力法缓存优化

#include<iostream>
#include<vector>
using namespace std;

int main(){
    int x, y, z;
    while(cin >> x >> y >> z){
        vector<vector<int> > A(x, vector<int>(y, 0));
        vector<vector<int> > B(y, vector<int>(z, 0));
        for(int i = 0; i < x; i++) //输入两个矩阵
            for(int j = 0; j < y; j++)
                cin >> A[i][j];
        for(int i = 0; i < y; i++)
            for(int j = 0; j < z; j++)
                cin >> B[i][j];
        vector<vector<int> > C(x, vector<int>(z, 0)); //构建结果矩阵
        int temp;
        for(int i = 0; i < x; i++)
            for(int k = 0; k < y; k++){
                temp = A[i][k];  //优先访问这个元素
                for(int j = 0; j < z; j++)
                    C[i][j] += temp * B[k][j]; //行*列相加，这一行访问不中断
            }
        for(int i = 0; i < x; i++){ //输出
            for(int j = 0; j < z; j++)
                cout << C[i][j] << " ";
            cout << endl;
        }
    }
    return 0;
}

HJ70 矩阵乘法计算量估算

描述

矩阵乘法的运算量与矩阵乘法的顺序强相关。
例如：

A是一个50×10的矩阵，B是10×20的矩阵，C是20×5的矩阵

计算ABC有两种顺序：((AB)C)或者(A(BC))，前者需要计算15000次乘法，后者只需要3500次。

编写程序计算不同的计算顺序需要进行的乘法次数。

数据范围：矩阵个数：1≤n≤15 ，行列数：1≤rowi,coli≤100 ，保证给出的字符串表示的计算顺序唯一。

进阶：时间复杂度：O(n) ，空间复杂度：O(n)

输入描述：

输入多行，先输入要计算乘法的矩阵个数n，每个矩阵的行数，列数，总共2n的数，最后输入要计算的法则
计算的法则为一个字符串，仅由左右括号和大写字母（'A'~'Z'）组成，保证括号是匹配的且输入合法！

输出描述：

输出需要进行的乘法次数

方法一：栈方法

#include <iostream>
#include <vector>
#include <stack>

using namespace std;

int main() {
    int n;
    while(cin >> n) {
        string rule;
        vector<pair<int, int>> matrix;
        for (int i = 0; i < n; ++i) {//输入n个矩阵的行数和列数
            pair<int, int> temp;
            cin >> temp.first >> temp.second;
            matrix.push_back(temp);
        }
        cin >> rule;//输入计算法则
        stack<pair<int, int>> stk;
        int ans = 0, k = 0;
        for (int i = 0; i < rule.size(); ++i) {//遍历一遍计算法则
            if (rule[i] == ')') {//当为右括号时从栈中取出两个矩阵计算
                pair<int, int> y = stk.top();
                stk.pop();
                pair<int, int> x = stk.top();
                stk.pop();
                ans += x.first * x.second * y.second;//计算量
                pair<int, int> temp(x.first, y.second);//结果矩阵的大小
                stk.push(temp);
            } else if(rule[i] != '('){
                stk.push(matrix[k]);//当前为字母时，矩阵进栈
                k++;
            }
        }
        cout << ans <<endl;
    }
    return 0;
}

方法二：递归

#include<iostream>
#include<stack>
#include<string>
#include<vector>
#include<map>

using namespace std;

map<char, pair<int, int> > matrix;//矩阵和大小之间的映射
int count;//计算量

pair<int, int> compute(string str){
    stack<pair<int, int> > stk; //记录尚未计算的矩阵
    str = str.substr(1, str.size()-2);//去掉首位的两个括号
    for(int i = 0; i < str.size();i++){
        if(str[i] == '('){ //如果是左括号，需要递归计算
            int layer = 0; 
            int j = i;
            while(j <= str.size()){//找到和当前左括号匹配的右括号
                if(str[j] == '('){
                    layer++;
                }else if(str[j] == ')'){
                    layer--;
                }
                if(layer == 0){
                    break;
                }
                j++;
            }
            pair<int, int> res = compute(str.substr(i, j - i + 1));//递归计算括号中的部分
            i = j ;//从括号后面的内容继续遍历
            if(stk.empty()){ //如果stk为空，表示当前得到的矩阵是第一个矩阵，需要存下，等待下一个矩阵计算
                stk.push(res);
            }else{ //若stk不为空，需要计算
                pair<int, int> temp = stk.top();
                stk.pop();
                count += temp.first * temp.second * res.second;
                stk.push(make_pair(temp.first,res.second));//更新栈中的值
            }
        }else if(isupper(str[i])){ //如果是矩阵的话
            if(stk.empty()){ //stk为空，进入到stk中
                stk.push(matrix[str[i]]);
            }else{ //如果栈不为空，需要计算
                pair<int, int> temp = stk.top();
                stk.pop();
                count += temp.first * temp.second * matrix[str[i]].second;
                stk.push(make_pair(temp.first,matrix[str[i]].second));//更新栈中的值
            }
        }
    }
    return stk.top(); //遍历一遍结束，返回当前计算的矩阵大小
}

int main(){
    int n;
    while(cin >> n){
        count = 0;
        string rule;
        char ch = 'A';
        for(int i = 0; i < n; i++){ //输入n个矩阵的行列数
            cin >> matrix[ch].first >> matrix[ch].second;
            ch++;
        }
        cin >> rule;  //输入运算法则
        stack<char> s; //记录代表矩阵的字符
        compute(rule);
        cout << count << endl;
    }
    return 0;
}

HJ71 字符串通配符

描述

问题描述：在计算机中，通配符一种特殊语法，广泛应用于文件搜索、数据库、正则表达式等领域。现要求各位实现字符串通配符的算法。
要求：
实现如下2个通配符：
：匹配0个或以上的字符（注：能被和?匹配的字符仅由英文字母和数字0到9组成，下同）
？：匹配1个字符

注意：匹配时不区分大小写。

输入：
通配符表达式；
一组字符串。

输出：

返回不区分大小写的匹配结果，匹配成功输出true，匹配失败输出false

数据范围：字符串长度：1≤s≤100

进阶：时间复杂度：O(n^2)，空间复杂度：O(n)

输入描述：

先输入一个带有通配符的字符串，再输入一个需要匹配的字符串

输出描述：

返回不区分大小写的匹配结果，匹配成功输出true，匹配失败输出false

方法一：动态规划

#include<string>
#include<iostream>
#include<vector>

using namespace std;

int match_string(string str,string pattern){
    int len1 = str.size();
    int len2 = pattern.size();
    vector<vector<int> > dp(len2+1,vector<int>(len1+1,0));
    //多加一行一列作为初始初值所用
    dp[0][0] = 1;//初始化
    for(int i=1;i <=len2;i++){
        char ch1 = pattern[i-1];
        ////设置每次循环的初值，即当星号不出现在首位时，匹配字符串的初值都为false
        dp[i][0] = dp[i-1][0]&&(ch1=='*');
        for(int j=1;j<=len1;j++){
            char ch2 = str[j-1];
        	if(ch1=='*'){
                dp[i][j]=dp[i-1][j]||dp[i][j-1]; //当匹配字符为*号时，可以匹配0个或者多个
            }else{
                if(isalpha(ch2)){//ch2为字母时，尝试是否能匹配
                    dp[i][j]=dp[i-1][j-1]&&(ch1=='?'||(ch2==ch1||ch2==(ch1+('A'-'a'))||ch2==(ch1-('A'-'a'))));
                }else if(isdigit(ch2)){//ch2为数字时，尝试是否能匹配
                    dp[i][j]=dp[i-1][j-1]&&(ch1=='?'||(ch1==ch2));
                }else {//ch2既不为字母也不为数字时，只有ch1和ch2相同才能匹配
                    dp[i][j]=dp[i-1][j-1]&&(ch1==ch2);
                }
            }

    	}
    }
    return dp[len2][len1];
}

int main(){
    string str1,str2;
    while(cin >> str1 >> str2){
       int flag =  match_string(str2,str1);
       if(flag){
           cout << "true" << endl;
       }else{
           cout << "false" << endl;
       }
    }
    
}

方法二：递归

#include<bits/stdc++.h>
using namespace std;

bool match(const char* s,const char* p){

    //两个字符串同时结束,返回true
    if((*p=='\0')&&(*s=='\0')){
        return true;
    }
     //两个字符串中有一个先结束，返回false
    if((*p=='\0')||(*s=='\0')){
        return false;
    }
    if(*p=='?'){//通配符为？时
        if(!isdigit(*s)&&!isalpha(*s)){//只能匹配数字或字母
            return false;
        }
        //匹配一个字符，从下一个位置开始继续匹配
        return match(s+1,p+1);
    }else if(*p=='*'){//通配符为！时
        while(*p=='*'){//多个*和一个*效果相同
            p++;
        }
        p--;
        //遇到*号，匹配0个（str+1,str1不用动），匹配1个（str和str1都往前移动1位），匹配多个（str不用动，str+1）
        return match(s,p+1) || match(s+1,p+1) ||  match(s+1,p);
    }else if(tolower(*p)==tolower(*s)){//不区分大小写
         //当前两字符相等，则进行下一个字符的匹配
        return match(s+1,p+1);
    }
    return false;//不满足上述三种情况，不匹配

}



int main(){
    string p,s;
    while(cin>>p>>s){
        bool res = match(s.c_str(),p.c_str());
        if(res){
            cout<<"true"<<endl;
        }else{
            cout<<"false"<<endl;
        }
    }
    return 0;
}

HJ72 百钱买百鸡问题

描述

公元五世纪，我国古代数学家张丘建在《算经》一书中提出了“百鸡问题”：鸡翁一值钱五，鸡母一值钱三，鸡雏三值钱一。百钱买百鸡，问鸡翁、鸡母、鸡雏各几何？

现要求你打印出所有花一百元买一百只鸡的方式。

输入描述：

输入任何一个整数，即可运行程序。

输出描述：

输出有数行，每行三个整数，分别代表鸡翁，母鸡，鸡雏的数量

方法一：数学办法

#include<iostream>
using namespace std;

//鸡翁、鸡母、鸡雏分别为x, y, z 三个变量。
//x+y+z=100
//5x+3y+z/3=100
//确定x即可算出y和z，若y和z为非负整数，则为有效结果，输出。

int main(){
     
    for(int x=0;x<=14;x++){//解方程，计算x的范围是[0,14],枚举x
        if((100-7*x)%4==0){
            int y=(100-7*x)/4;//求解y,z
            int z=100-x-y;
            printf("%d %d %d\n",x,y,z);
        }
    }
    return 0;
}

方法二：暴力法

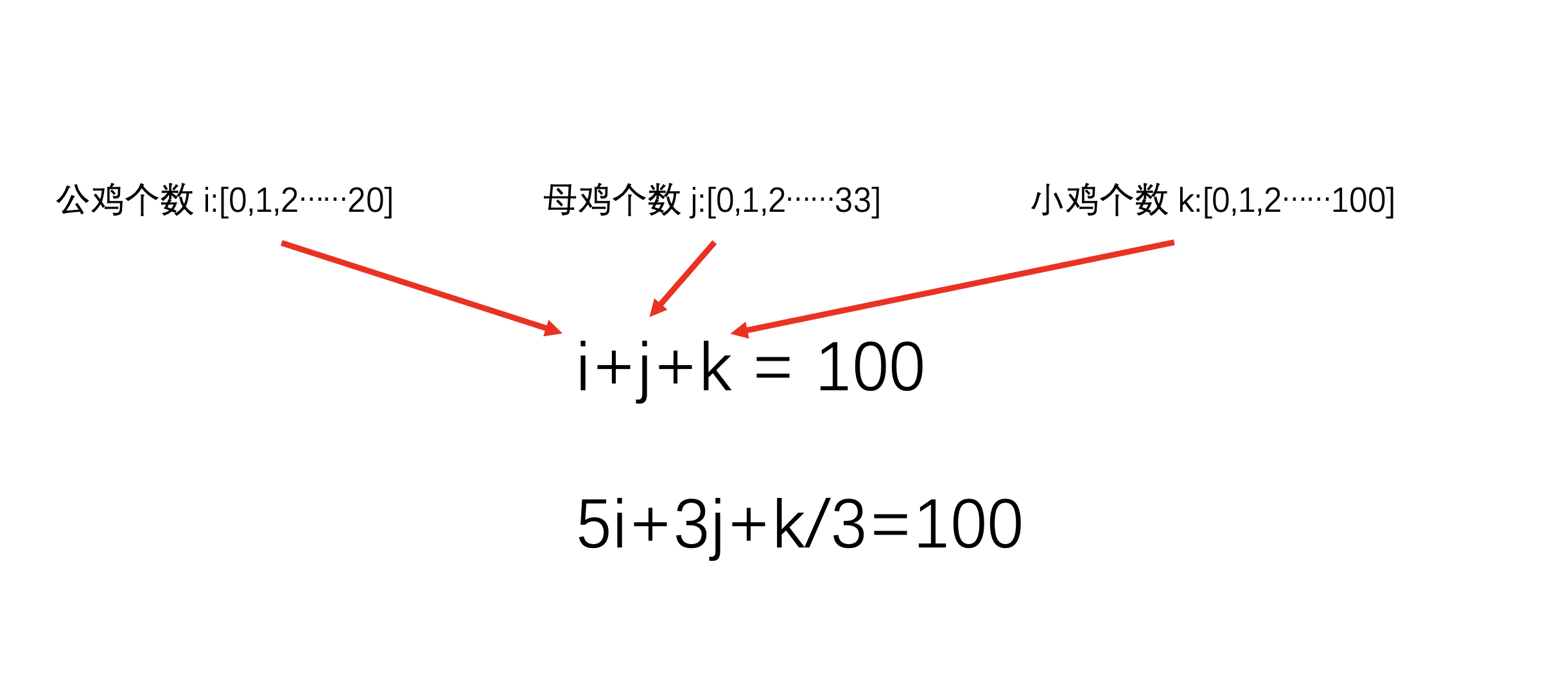
#include<iostream>
using namespace std;
 
int main(){
    for(int i = 0; i <= 20; i++) {
        for(int j = 0; j <= 33; j++) {
            for(int k = 0; k <= 100; k++){ //遍历所有可能的公鸡、母鸡、小鸡取值
                if(i + j + k == 100 && 5 * i + 3 * j + double(k) / 3 == 100) {//鸡的总数等于100，且总共花了100元
                    cout << i << " " << j << " " << k << endl;
                }
            }
        }
    }
    return 0;
}

HJ73 计算日期到天数转换

描述

根据输入的日期，计算是这一年的第几天。

保证年份为4位数且日期合法。

进阶：时间复杂度：O(n)，空间复杂度：O(1)\

输入描述：

输入一行，每行空格分割，分别是年，月，日

输出描述：

输出是这一年的第几天

方法一：数组法

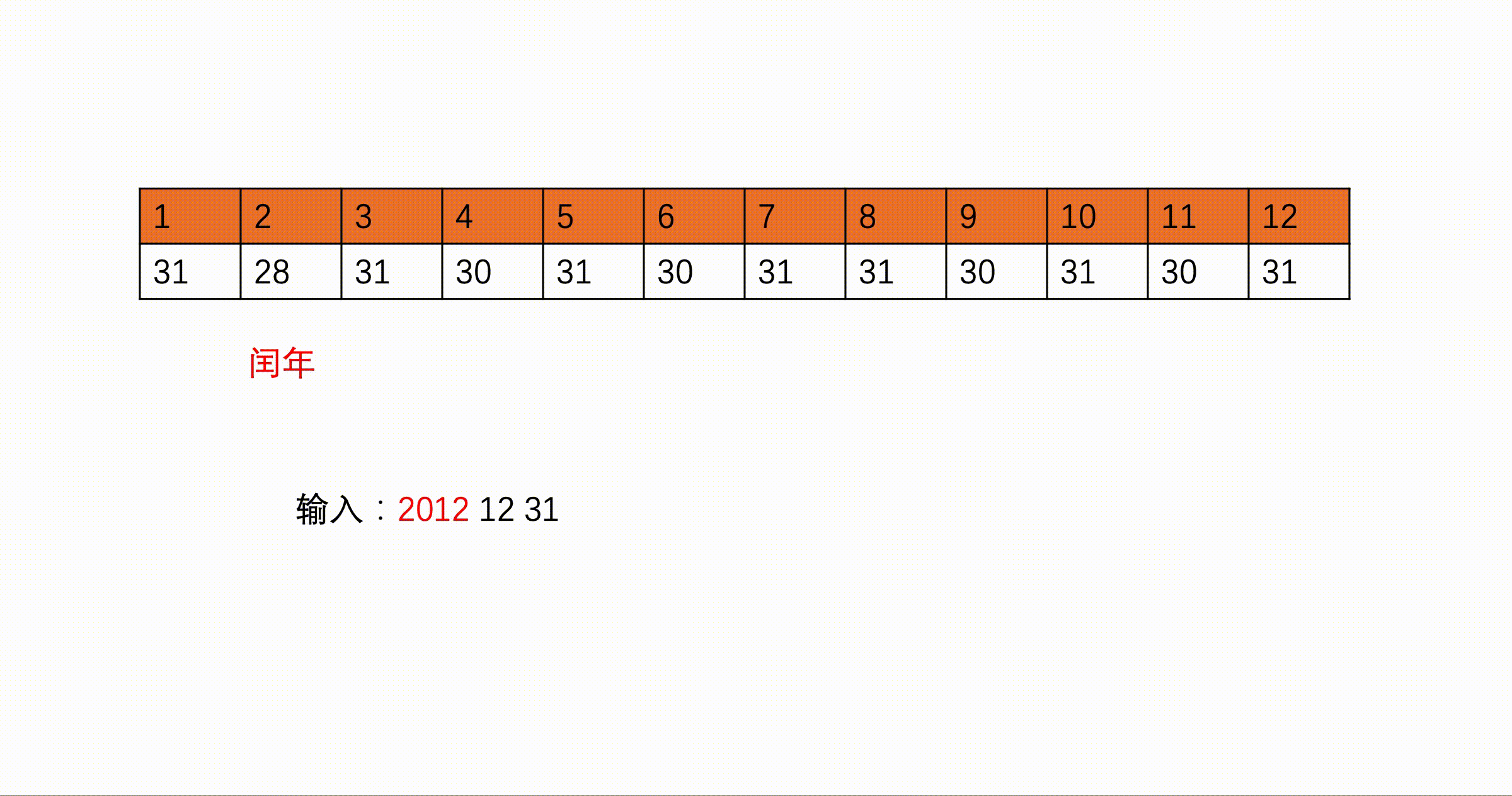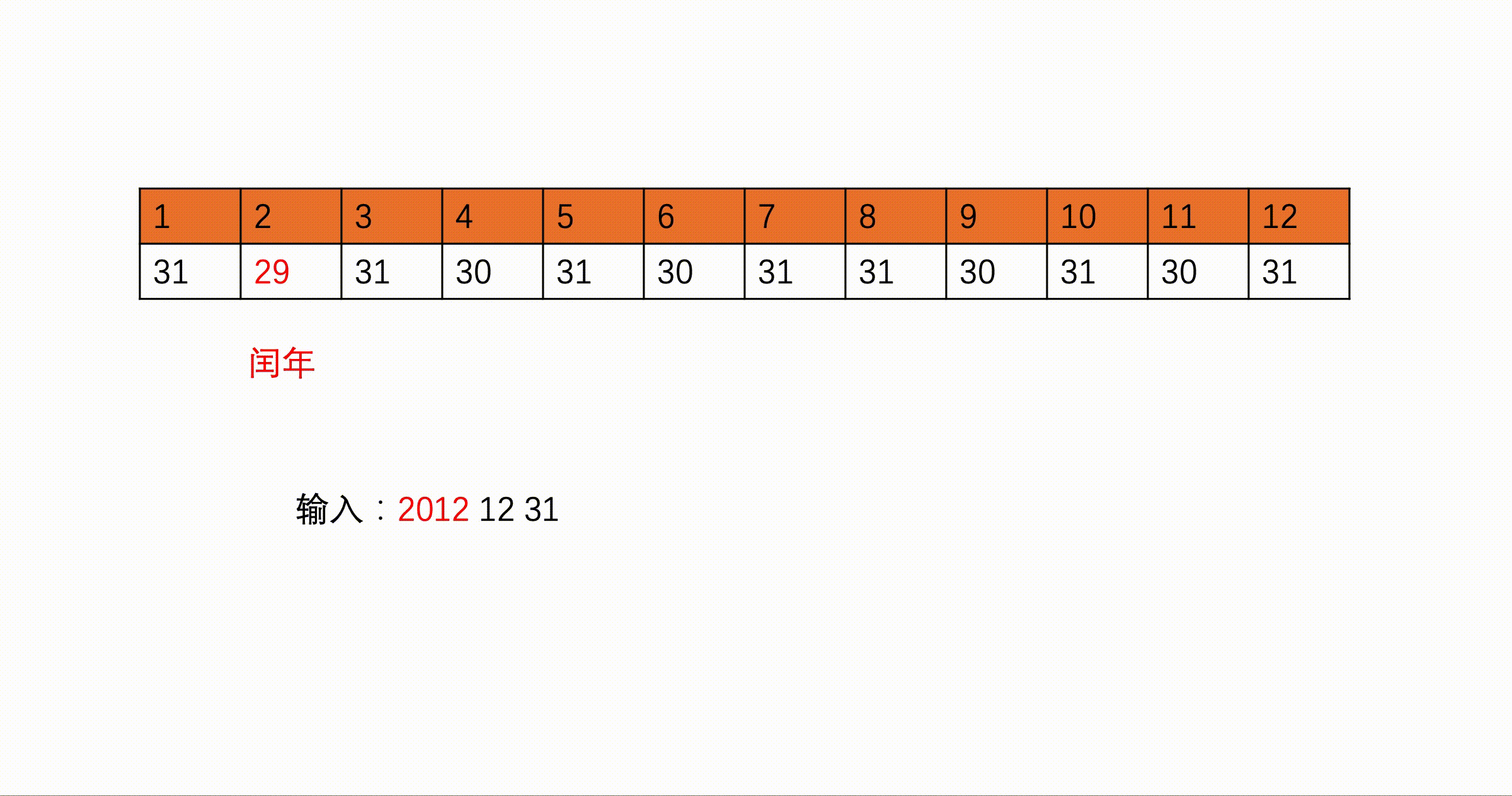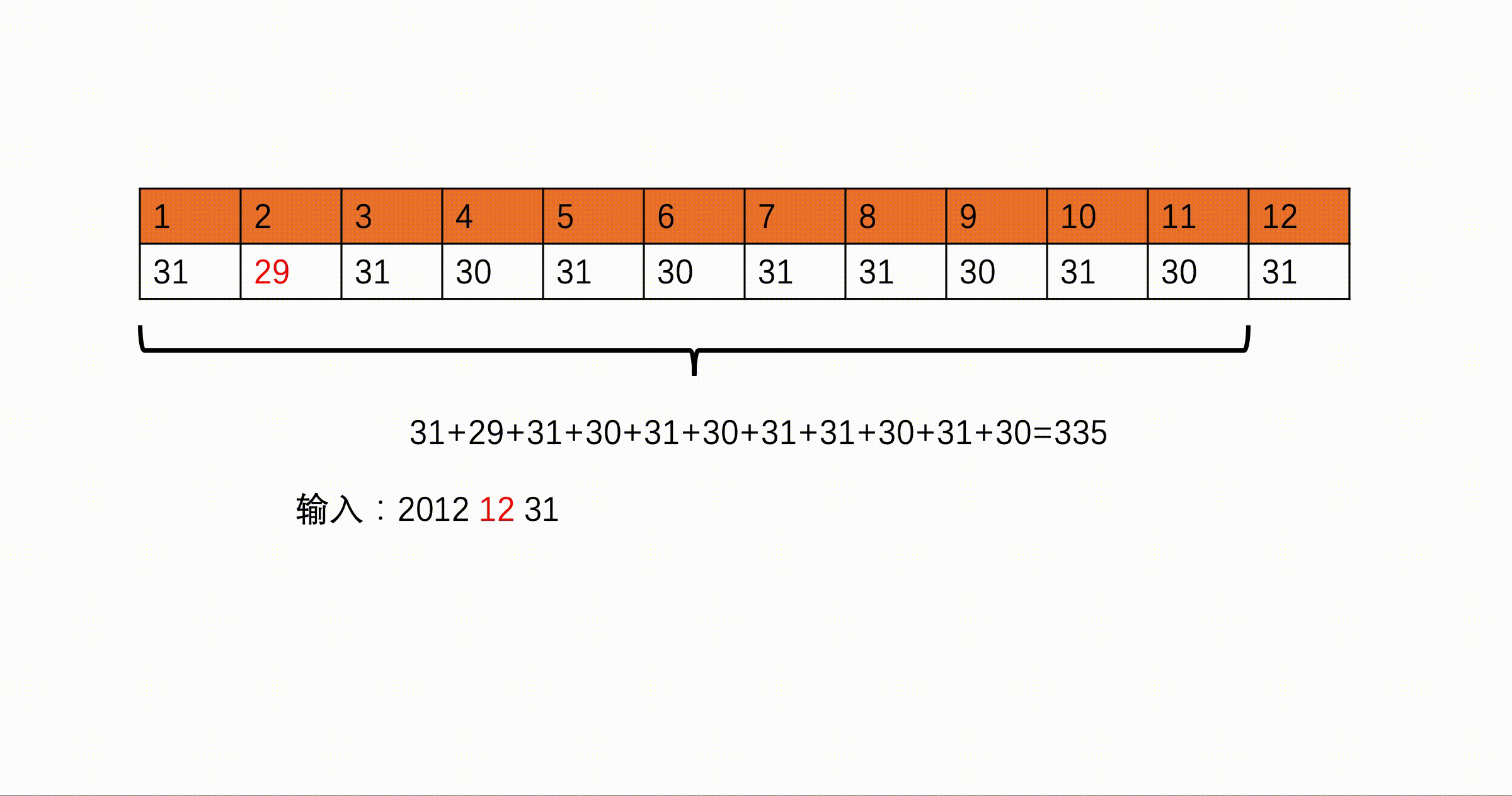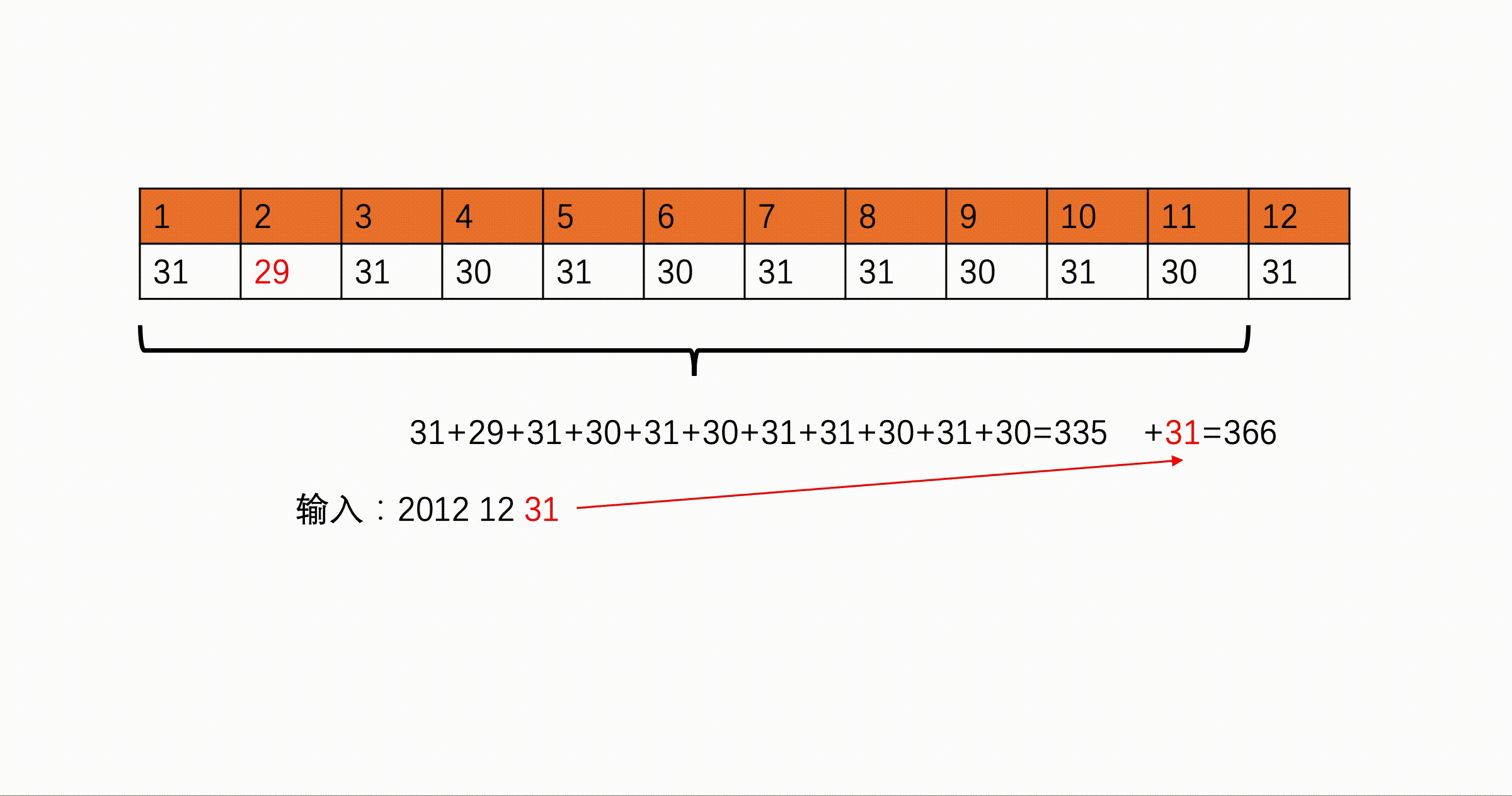
#include <iostream>
using namespace std;
int main(){
    int year,month,day;
    cin>>year>>month>>day;
    int count=0;//统计天数
    int monthday[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};//monthday[i]表示第i月的天数
    if(year%400==0||(year%4==0&&year%100!=0)){//当前月份大于两个月且为闰年时，二月有29天
        monthday[2]=29;
    }
    for(int i=1;i<=month-1;i++){//统计到当前月份的天数
      count=count+monthday[i];
    }
    count=count+day;//加上当前月的天数
    cout<<count;
}

方法二：

#include<iostream>
#include<string>

using namespace std;

int main(){
    int year,month,day;
    int res;
    int flag=0;
    int num[12]={31,59,90, 120, 151, 181, 212, 243, 273, 304, 334, 365};//num[i]表示第i+1个月结束后的天数
    while(cin>>year>>month>>day){
        if(year%4==0 && year%100!=0){//如果是闰年
            flag=1;
        }
        if(month<=2){
            if(month == 1){
                res = day;
            }else{
                res = num[0] + day;
            }
        }else{//超过2月就要考虑是否为闰年了
            res=num[month-2]+day+flag;
        }
        flag=0;
        cout<<res<<endl;
    }
}

HJ74 参数解析

描述

在命令行输入如下命令：

xcopy /s c:\ d:\e，

各个参数如下：

参数1：命令字xcopy

参数2：字符串/s

参数3：字符串c:\

参数4: 字符串d:\e

请编写一个参数解析程序，实现将命令行各个参数解析出来。

解析规则：

1.参数分隔符为空格
2.对于用""包含起来的参数，如果中间有空格，不能解析为多个参数。比如在命令行输入xcopy /s "C:\program files" "d:"时，参数仍然是4个，第3个参数应该是字符串C:\program files，而不是C:\program，注意输出参数时，需要将""去掉，引号不存在嵌套情况。
3.参数不定长

4.输入由用例保证，不会出现不符合要求的输入

数据范围：字符串长度：1≤s≤1000

进阶：时间复杂度：O(n) ，空间复杂度：O(n)

输入描述：

输入一行字符串，可以有空格

输出描述：

输出参数个数，分解后的参数，每个参数都独占一行

方法一：字符连接

#include<iostream>
#include<string>
#include<vector>
using namespace std;

int main(){
    string s;
    while(getline(cin, s)){
        vector<string> output;
        string temp = "";
        bool flag = false; //记录是否进入引号中
        for(int i = 0; i < s.length(); i++){
            if(flag){ //如果在引号中
                if(s[i] != '\"') //遇到非引号都添加为字符串
                    temp += s[i];
                else flag = false; //否则设置出引号
            }else{ //如果不在引号中
                if(s[i] == ' '){ //遇到空格隔断
                    output.push_back(temp); 
                    temp = "";
                }else if(s[i] == '\"') //遇到引号设置为进入引号
                    flag = true; 
                else //其余添加进字符串
                    temp += s[i];
            }
        }
        output.push_back(temp); //最后一段
        cout << output.size() << endl; //输出参数个数
        for(int i = 0; i < output.size(); i++)
            cout << output[i] << endl;
    }
    return 0;
}

方法二：字符串截取

#include<iostream>
#include<string>
#include<vector>
using namespace std;

int main(){
    string s;
    while(getline(cin, s)){
        vector<string> output;
        int p = 0;
        bool flag = false; //记录是否进入引号中
        for(int i = 0; i < s.length(); i++){
            if(s[i] == '\"'){ //遇到引号
                if(!flag) //第一个引号
                    flag = true;
                else{ //第二个引号
                    flag = false;
                    output.push_back(s.substr(p, i - p)); //截取字符串加入
                }
                p = i + 1;
            } else if(s[i] == ' ' && !flag){ //遇到引号外的空格
                if(i != p)  //非空字符串
                    output.push_back(s.substr(p, i - p)); //截取字符串加入
                p = i + 1;
            } else if(i == s.length() - 1) //最后一个参数字符串
                output.push_back(s.substr(p, i - p + 1));
        }
        cout << output.size() << endl; //输出参数个数
        for(int i = 0; i < output.size(); i++)
            cout << output[i] << endl;
    }
    return 0;
}

HJ75 公共子串计算

描述

给定两个只包含小写字母的字符串，计算两个字符串的最大公共子串的长度。

注：子串的定义指一个字符串删掉其部分前缀和后缀（也可以不删）后形成的字符串。

数据范围：字符串长度：1≤s≤150

进阶：时间复杂度：O(n^3)，空间复杂度：O(n)

输入描述：

输入两个只包含小写字母的字符串

输出描述：

输出一个整数，代表最大公共子串的长度

方法一：枚举法

#include<iostream>
#include<string>
#include<math.h>

using namespace std;

int main(){
    string a,b;
    while(cin>>a>>b){//输入两个字符串
      int maxLen=0;
      for(int i=0;i<a.size();i++){
          for(int j=i;j<a.size();j++){
              string temp=a.substr(i,j-i+1);//temp为a的子串
              if(int(b.find(temp))<0){//若temp在b中没有出现，跳出当前循环，从下一个位置i开始找子串
                  break;
              }else if(maxLen<temp.size()){//找到了更长的公共子串
                  maxLen=temp.size();
              }
          }
      }
        cout<<maxLen<<endl;
    }
    return 0;
}

方法二：动态规划

#include <iostream>
#include <vector>

using namespace std;

int main(){
    string a,b;
    while (cin >> a >> b)
    {
        int maxLen = 0;
        vector<vector<int>> dp(b.size()+1,vector<int>(a.size()+1,0));//动态数组，dp[i][j]表示b以第i个字符结尾，a以第j个字符结尾的公共子串的长度
        for (int i = 1; i <= b.size(); ++i){
            for (int j = 1; j <= a.size(); ++j){
                if (b[i - 1] == a[j - 1]) {//b中第i个字符和a中第j个字符相同
                    dp[i][j] = dp[i - 1][j - 1] + 1;//前一个长度加一
                }else {
                    dp[i][j] = 0;//如果第i个字符和第j个字符不同，则以他们结尾的子串不可能相同
                }
                if (maxLen < dp[i][j]) {//更新最大值
                    maxLen = dp[i][j];
                }
            }
        }
        cout << maxLen << endl;
    }
    return 0;
}

续[[华为机试76-90]]

已到达文章底部，欢迎留言、表情互动~

0
赞一个
0
支持下
0
有点酷
0
啥玩意
0
看不懂

昵称

邮箱

网址

按正序
按倒序
按热度

HJ61 放苹果

# HJ61 放苹果

# 描述

# 输入描述：

# 输出描述：

# 解法一：dfs

# 解法二：动态规划

# HJ62 查找输入整数二进制中1的个数

# 描述

# 输入描述：

# 输出描述：

# 解法一：运用位运算进行操作

# 解法二： STL容器

# 方法三：转化二进制字符串

# 方法四：移位运算和位与运算

# 方法五：位与运算去掉二进制末尾1

# 方法六：库函数

# HJ63 DNA序列

# 描述

# 输入描述：

# 输出描述：

# 方法一：暴力解法

# 方法二：滑动窗口

# HJ64 MP3光标位置

# 描述

# 输入描述：

# 输出描述：

# 方法一：模拟

# 方法二：滑动窗口

# HJ65 查找两个字符串a,b中的最长公共子串

# 描述

# 输入描述：

# 输出描述：

# 方法一：暴力枚举

# 方法二：枚举改进

# 方法三：动态规划

# HJ66 配置文件恢复

# 描述

# 输入描述：

# 输出描述：

# 方法一：模拟存储

# 方法二： 正则表达式

# HJ67 24点游戏算法

# 描述

# 输入描述：

# 输出描述：

# 方法一：穷举遍历

# 方法二：递归搜索

# HJ68 成绩排序

# 描述

# 输入描述：

# 输出描述：

# 方法一：库函数

# 方法二：桶排序

# HJ69 矩阵乘法

# 输入描述：

# 输出描述：

# 方法一：

# 方法二：

# 方法三：暴力法

# 方法四：暴力法缓存优化

# HJ70 矩阵乘法计算量估算

# 描述

# 输入描述：

# 输出描述：

# 方法一：栈方法

# 方法二：递归

# HJ71 字符串通配符

# 描述

# 输入描述：

# 输出描述：

# 方法一：动态规划

# 方法二：递归

# HJ72 百钱买百鸡问题

# 描述

# 输入描述：

# 输出描述：

# 方法一：数学办法

# 方法二： 暴力法

# HJ73 计算日期到天数转换

HJ61 放苹果

描述

输入描述：

输出描述：

解法一：dfs

解法二：动态规划

HJ62 查找输入整数二进制中1的个数

描述

输入描述：

输出描述：

解法一：运用位运算进行操作

解法二： STL容器

方法三：转化二进制字符串

方法四：移位运算和位与运算

方法五：位与运算去掉二进制末尾1

方法六：库函数

HJ63 DNA序列

描述

输入描述：

输出描述：

方法一：暴力解法

方法二：滑动窗口

HJ64 MP3光标位置

描述

输入描述：

输出描述：

方法一：模拟

方法二：滑动窗口

HJ65 查找两个字符串a,b中的最长公共子串

描述

输入描述：

输出描述：

方法一：暴力枚举

方法二：枚举改进

方法三：动态规划

HJ66 配置文件恢复

描述

输入描述：

输出描述：

方法一：模拟存储

方法二：正则表达式

HJ67 24点游戏算法

描述

输入描述：

输出描述：

方法一：穷举遍历

方法二：递归搜索

HJ68 成绩排序

描述

输入描述：

输出描述：

方法一：库函数

方法二：桶排序

HJ69 矩阵乘法

输入描述：

输出描述：

方法一：

方法二：

方法三：暴力法

方法四：暴力法缓存优化

HJ70 矩阵乘法计算量估算

描述

输入描述：

输出描述：

方法一：栈方法

方法二：递归

HJ71 字符串通配符

描述

输入描述：

输出描述：

方法一：动态规划

方法二：递归

HJ72 百钱买百鸡问题

描述

输入描述：

输出描述：

方法一：数学办法

方法二：暴力法

HJ73 计算日期到天数转换

描述